


Next: ЧаÑÑиÑное ÑоÑ
Ñанение акÑиалÑнÑÑ
Ñоков
Up: ÐекÑÐ¸Ñ 9. ÐиÑалÑÐ½Ð°Ñ ÑиммеÑÑиÑ
Previous: ÐевÑе и пÑавÑе кваÑки
РаÑÑмоÑÑим маÑÑиÑнÑе ÑлеменÑÑ ÑоÑ
ÑанÑÑÑиÑ
ÑÑ Ð²ÐµÐºÑоÑнÑÑ
и акÑиалÑнÑÑ
Ñоков.
ÐÑÑÑÑ Ð²ÐµÐºÑоÑнÑй Ñок бÑдеÑ, напÑимеÑ, ÑлекÑÑомагниÑнÑм Ñоком
где
 , а ÑоÑÑоÑние - пÑоÑоном. РпÑеделе
нÑлевой пеÑедаÑи импÑлÑÑа
, а ÑоÑÑоÑние - пÑоÑоном. РпÑеделе
нÑлевой пеÑедаÑи импÑлÑÑа
 Ð´Ð»Ñ Ð¼Ð°ÑÑиÑного ÑлеменÑа
ÑлекÑÑомагниÑного Ñока по ÑоÑÑоÑÐ½Ð¸Ñ Ð¿ÑоÑона имеем
Ð´Ð»Ñ Ð¼Ð°ÑÑиÑного ÑлеменÑа
ÑлекÑÑомагниÑного Ñока по ÑоÑÑоÑÐ½Ð¸Ñ Ð¿ÑоÑона имеем
СоÑ
Ñанение Ñока ознаÑаеÑ, ÑÑо
ÐÑо ÑавенÑÑво вÑполнÑеÑÑÑ Ð² ÑÐ¸Ð»Ñ ÑÑÐ°Ð²Ð½ÐµÐ½Ð¸Ñ ÐиÑака Ð´Ð»Ñ Ð¿Ð¾Ð»Ñ Ð¿ÑоÑона.
РаÑÑмоÑÑим ÑепеÑÑ Ð°ÐºÑиалÑнÑй Ñок, оÑвеÑаÑÑий  -ÑаÑÐ¿Ð°Ð´Ñ Ð¿ÑоÑона
-ÑаÑÐ¿Ð°Ð´Ñ Ð¿ÑоÑона
ÐÑли Ð¼Ñ (по аналогии Ñ Ð²ÐµÐºÑоÑнÑм Ñоком) пÑедположим, ÑÑо маÑÑиÑнÑй
ÑÐ»ÐµÐ¼ÐµÐ½Ñ Ð¼ÐµÐ¶Ð´Ñ ÑоÑÑоÑниÑми нейÑÑона и пÑоÑона Ð¾Ñ Ð°ÐºÑиалÑного Ñока в
пÑеделе нÑлевой пеÑедаÑи импÑлÑÑа Ñавен
Ñо
ÑоÑ
Ñанение ÑÑого Ñока
ÑÑебÑеÑ
занÑÐ»ÐµÐ½Ð¸Ñ Ð¼Ð°ÑÑÑ Ð¿ÑоÑона  , ÑÑо пÑи ÑкÑпеÑименÑалÑном знаÑении
маÑÑÑ Ð¿ÑоÑона поÑÑдка
, ÑÑо пÑи ÑкÑпеÑименÑалÑном знаÑении
маÑÑÑ Ð¿ÑоÑона поÑÑдка  ознаÑало бÑ, ÑÑо киÑалÑÐ½Ð°Ñ ÑиммеÑÑиÑ
ÑилÑно наÑÑÑена.
ознаÑало бÑ, ÑÑо киÑалÑÐ½Ð°Ñ ÑиммеÑÑиÑ
ÑилÑно наÑÑÑена.
ÐÑ Ð¿Ñедположим, ÑÑо маÑÑиÑнÑй ÑÐ»ÐµÐ¼ÐµÐ½Ñ Ð¼ÐµÐ¶Ð´Ñ
ÑоÑÑоÑниÑми нейÑÑона и пÑоÑона Ð¾Ñ Ð°ÐºÑиалÑного Ñока в пÑеделе нÑлевой
пеÑедаÑи импÑлÑÑа Ñавен
Ñ.е. ÑоÑ
ÑанÑеÑÑÑ Ð°Ð²ÑомаÑиÑеÑки. ÐÑи  в
ÑÑом маÑÑиÑном ÑлеменÑе имееÑÑÑ Ð¿Ð¾Ð»ÑÑ, коÑоÑÑй оÑвеÑÐ°ÐµÑ ÑомÑ, ÑÑо
нейÑÑон излÑÑÐ°ÐµÑ Ð±ÐµÐ·Ð¼Ð°ÑÑовÑÑ Ð¿ÑевдоÑкалÑÑнÑÑ ÑаÑÑиÑÑ (
в
ÑÑом маÑÑиÑном ÑлеменÑе имееÑÑÑ Ð¿Ð¾Ð»ÑÑ, коÑоÑÑй оÑвеÑÐ°ÐµÑ ÑомÑ, ÑÑо
нейÑÑон излÑÑÐ°ÐµÑ Ð±ÐµÐ·Ð¼Ð°ÑÑовÑÑ Ð¿ÑевдоÑкалÑÑнÑÑ ÑаÑÑиÑÑ ( ),
пÑевÑаÑаеÑÑÑ Ð² пÑоÑон, а
),
пÑевÑаÑаеÑÑÑ Ð² пÑоÑон, а  аннигилиÑÑеÑÑÑ Ð°ÐºÑиалÑнÑм Ñоком.
аннигилиÑÑеÑÑÑ Ð°ÐºÑиалÑнÑм Ñоком.
ÐÐ°Ð¶Ð´Ð¾Ð¼Ñ Ð¸Ð· воÑÑми ÑоÑ
ÑанÑÑÑиÑ
ÑÑ Ð°ÐºÑиалÑнÑÑ
Ñоков оÑвеÑÐ°ÐµÑ Ñвой
безмаÑÑовÑй пÑевдоÑкалÑÑнÑй мезон. СиÑÑаÑиÑ, когда маÑÑÑ
пÑевдоÑкалÑÑнÑÑ
мезонов обÑаÑаÑÑÑÑ Ð² Ð½Ð¾Ð»Ñ Ð² киÑалÑном пÑеделе нÑлевÑÑ
маÑÑ ÐºÐ²Ð°Ñков, кажеÑÑÑ ÑизиÑеÑки более инÑеÑеÑной, Ñ.к. на опÑÑе вÑе
воÑÐµÐ¼Ñ Ð¿ÑевдоÑкалÑÑнÑÑ
мезонов ÑÑÑеÑÑвенно легÑе оÑÑалÑнÑÑ
адÑонов.
ÐÑобенно ÑÑо ÑпÑаведливо в оÑноÑении 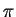 -мезонов. Таким обÑазом
киÑалÑнÑÑ ÑиммеÑÑÐ¸Ñ Ð¼Ð¾Ð¶Ð½Ð¾ ÑеализоваÑÑ, Ñделав безмаÑÑовÑми ÑолÑко
окÑÐµÑ Ð¿ÑевдоÑкалÑÑнÑÑ
мезонов.
-мезонов. Таким обÑазом
киÑалÑнÑÑ ÑиммеÑÑÐ¸Ñ Ð¼Ð¾Ð¶Ð½Ð¾ ÑеализоваÑÑ, Ñделав безмаÑÑовÑми ÑолÑко
окÑÐµÑ Ð¿ÑевдоÑкалÑÑнÑÑ
мезонов.
ÐекÑоÑнÑе заÑÑÐ´Ñ  , дейÑÑвÑÑ Ð½Ð°
ÑаÑÑиÑÑ Ð¸Ð· окÑеÑа баÑионов, напÑимеÑ, пеÑеводÑÑ Ð¸Ñ
дÑÑг в дÑÑга.
ÐкÑиалÑнÑй заÑÑд
, дейÑÑвÑÑ Ð½Ð°
ÑаÑÑиÑÑ Ð¸Ð· окÑеÑа баÑионов, напÑимеÑ, пеÑеводÑÑ Ð¸Ñ
дÑÑг в дÑÑга.
ÐкÑиалÑнÑй заÑÑд  , дейÑÑвÑÑ, Ñкажем, на пÑоÑон, пеÑÐµÐ²Ð¾Ð´Ð¸Ñ ÐµÐ³Ð¾
в ÑоÑÑоÑние Ñ Ñем же Ñпином, изоÑпином, заÑÑдом, гипеÑзаÑÑдом, но Ñ
пÑоÑивоположной ÑеÑноÑÑÑÑ. Такого ÑоÑÑоÑÐ½Ð¸Ñ Ð² окÑеÑе баÑионов неÑ,
ÑÑо двÑÑ
ÑаÑÑиÑное ÑоÑÑоÑние "
, дейÑÑвÑÑ, Ñкажем, на пÑоÑон, пеÑÐµÐ²Ð¾Ð´Ð¸Ñ ÐµÐ³Ð¾
в ÑоÑÑоÑние Ñ Ñем же Ñпином, изоÑпином, заÑÑдом, гипеÑзаÑÑдом, но Ñ
пÑоÑивоположной ÑеÑноÑÑÑÑ. Такого ÑоÑÑоÑÐ½Ð¸Ñ Ð² окÑеÑе баÑионов неÑ,
ÑÑо двÑÑ
ÑаÑÑиÑное ÑоÑÑоÑние " нÑклон". ÐÑи ÑÑом
нÑклон". ÐÑи ÑÑом 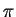 -мезон
Ð¸Ð¼ÐµÐµÑ Ð½ÑлевÑÑ ÑнеÑгиÑ, Ñак ÑÑо ÑоÑÑоÑÐ½Ð¸Ñ "нÑклон" и "
-мезон
Ð¸Ð¼ÐµÐµÑ Ð½ÑлевÑÑ ÑнеÑгиÑ, Ñак ÑÑо ÑоÑÑоÑÐ½Ð¸Ñ "нÑклон" и " нÑклон"
вÑÑожденÑ, как и должно бÑÑÑ, еÑли имееÑÑÑ ÑиммеÑÑиÑ. ТакаÑ
ÑеализаÑÐ¸Ñ ÑиммеÑÑии назÑваеÑÑÑ Ð½ÐµÐ»Ð¸Ð½ÐµÐ¹Ð½Ð¾Ð¹.
нÑклон"
вÑÑожденÑ, как и должно бÑÑÑ, еÑли имееÑÑÑ ÑиммеÑÑиÑ. ТакаÑ
ÑеализаÑÐ¸Ñ ÑиммеÑÑии назÑваеÑÑÑ Ð½ÐµÐ»Ð¸Ð½ÐµÐ¹Ð½Ð¾Ð¹.
Sergei B. Popov
2001-05-29



