


Next: ÐадаÑа 9
Up: ÐекÑÐ¸Ñ 9. ÐиÑалÑÐ½Ð°Ñ ÑиммеÑÑиÑ
Previous: ÐÐµÐ»Ð¸Ð½ÐµÐ¹Ð½Ð°Ñ ÑеализаÑÐ¸Ñ ÐºÐ¸ÑалÑной ÑиммеÑÑии
ÐанÑление маÑÑ
пÑевдоÑкалÑÑнÑÑ
мезонов в пÑеделе нÑлевÑÑ
маÑÑ ÐºÐ²Ð°Ñков можно ÑвидеÑÑ,
ÑаÑÑмаÑÑÐ¸Ð²Ð°Ñ Ð¼Ð°ÑÑиÑнÑе ÑлеменÑÑ Ð°ÐºÑиалÑнÑÑ
Ñоков междÑ
ÑооÑвеÑÑÑвÑÑÑими пÑевдоÑкалÑÑнÑми мезонами и вакÑÑмом. ÐапÑимеÑ,
Ð´Ð»Ñ  -мезона маÑÑиÑнÑй ÑлеменÑ
-мезона маÑÑиÑнÑй ÑлеменÑ
вÑ
Ð¾Ð´Ð¸Ñ Ð²
амплиÑÑÐ´Ñ Ñлабого ÑаÑпада
 .
ÐÑÑиÑлÑÑ Ð´Ð¸Ð²ÐµÑгенÑÐ¸Ñ Ð°ÐºÑиалÑного Ñока, полÑÑаем
.
ÐÑÑиÑлÑÑ Ð´Ð¸Ð²ÐµÑгенÑÐ¸Ñ Ð°ÐºÑиалÑного Ñока, полÑÑаем
оÑкÑда видно, ÑÑо маÑÑа 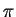 -мезона занÑлÑеÑÑÑ Ð¿Ñи занÑлении маÑÑ
кваÑков
-мезона занÑлÑеÑÑÑ Ð¿Ñи занÑлении маÑÑ
кваÑков
 ÐналогиÑно
ÐналогиÑно
СÑиÑаÑ, ÑÑо
 и
и
 (
(
 ÑкÑпеÑименÑалÑно), Ð´Ð»Ñ Ð¼Ð°ÑÑ ÐºÐ²Ð°Ñков полÑÑаем ÑооÑноÑение
ÑкÑпеÑименÑалÑно), Ð´Ð»Ñ Ð¼Ð°ÑÑ ÐºÐ²Ð°Ñков полÑÑаем ÑооÑноÑение
ÐÑли пÑинÑÑÑ, ÑÑо
 (Ñ
аÑакÑеÑнÑе ÑазноÑÑи маÑÑ Ð²
декÑплеÑе баÑионов), Ñо
(Ñ
аÑакÑеÑнÑе ÑазноÑÑи маÑÑ Ð²
декÑплеÑе баÑионов), Ñо
Ðам нÑжно еÑе
оÑениÑÑ  и
и  по оÑделÑноÑÑи. Ðо ÑиÑ
Ð¿Ð¾Ñ Ð¼Ñ Ð¸Ð³Ð½Ð¾ÑиÑовали
ÑлекÑÑомагниÑное взаимодейÑÑвие, коÑоÑое можеÑ, в ÑаÑÑноÑÑи, даваÑÑ
попÑавки к маÑÑам ÑаÑÑиÑ. ÐелиÑина ÑÑиÑ
попÑавок ÑÑавнима Ñ Ð¼Ð°ÑÑами
по оÑделÑноÑÑи. Ðо ÑиÑ
Ð¿Ð¾Ñ Ð¼Ñ Ð¸Ð³Ð½Ð¾ÑиÑовали
ÑлекÑÑомагниÑное взаимодейÑÑвие, коÑоÑое можеÑ, в ÑаÑÑноÑÑи, даваÑÑ
попÑавки к маÑÑам ÑаÑÑиÑ. ÐелиÑина ÑÑиÑ
попÑавок ÑÑавнима Ñ Ð¼Ð°ÑÑами
 -кваÑков. ÐоÑÑÐ¾Ð¼Ñ Ð½Ð°Ñе желание найÑи маÑÑÑ ÐºÐ²Ð°Ñков по
оÑделÑноÑÑи наÑалкиваеÑÑÑ Ð½Ð° необÑ
одимоÑÑÑ ÑÑеÑа ÑлекÑÑомагниÑнÑÑ
попÑавок. СделаÑÑ ÑколÑ-нибÑÐ´Ñ ÑÑÑого поÑледнее Ð¼Ñ Ð½Ðµ можем,
поÑÑÐ¾Ð¼Ñ Ð¾Ð³ÑаниÑимÑÑ ÑледÑÑÑей ÑпекÑлÑÑией. РдÑÑ
е полÑÑеннÑÑ
вÑÑе ÑооÑноÑений Ð¼ÐµÐ¶Ð´Ñ ÐºÐ²Ð°Ð´ÑаÑами маÑÑ Ð¿ÑевдоÑкалÑÑнÑÑ
мезонов
и маÑÑами кваÑков напиÑем ÑоÑмÑлÑ, ÑÑиÑÑваÑÑие Ñакже оÑлиÑие
заÑÑженнÑÑ
ÑаÑÑÐ¸Ñ Ð¾Ñ Ð½ÐµÐ¹ÑÑалÑнÑÑ
-кваÑков. ÐоÑÑÐ¾Ð¼Ñ Ð½Ð°Ñе желание найÑи маÑÑÑ ÐºÐ²Ð°Ñков по
оÑделÑноÑÑи наÑалкиваеÑÑÑ Ð½Ð° необÑ
одимоÑÑÑ ÑÑеÑа ÑлекÑÑомагниÑнÑÑ
попÑавок. СделаÑÑ ÑколÑ-нибÑÐ´Ñ ÑÑÑого поÑледнее Ð¼Ñ Ð½Ðµ можем,
поÑÑÐ¾Ð¼Ñ Ð¾Ð³ÑаниÑимÑÑ ÑледÑÑÑей ÑпекÑлÑÑией. РдÑÑ
е полÑÑеннÑÑ
вÑÑе ÑооÑноÑений Ð¼ÐµÐ¶Ð´Ñ ÐºÐ²Ð°Ð´ÑаÑами маÑÑ Ð¿ÑевдоÑкалÑÑнÑÑ
мезонов
и маÑÑами кваÑков напиÑем ÑоÑмÑлÑ, ÑÑиÑÑваÑÑие Ñакже оÑлиÑие
заÑÑженнÑÑ
ÑаÑÑÐ¸Ñ Ð¾Ñ Ð½ÐµÐ¹ÑÑалÑнÑÑ
Ð ÑазноÑÑÑÑ
неизвеÑÑнÑÑ ÑлекÑÑомагниÑнÑÑ Ð¿Ð¾Ð¿ÑÐ°Ð²ÐºÑ  можно
ÑокÑаÑиÑÑ, полÑÑив ÑооÑноÑение
можно
ÑокÑаÑиÑÑ, полÑÑив ÑооÑноÑение
Так как
 , Ñо
, Ñо
 и
и
 .
.
ÐÑ Ð²Ð¸Ð´Ð¸Ð¼, ÑÑо
 , поÑÑÐ¾Ð¼Ñ ÐºÐ¸ÑалÑнаÑ
, поÑÑÐ¾Ð¼Ñ ÐºÐ¸ÑалÑнаÑ
 -ÑиммеÑÑÐ¸Ñ ÑÐ°ÐºÐ°Ñ Ð¶Ðµ Ñ
оÑоÑаÑ, как обÑÑнаÑ
изоÑопиÑеÑкаÑ
-ÑиммеÑÑÐ¸Ñ ÑÐ°ÐºÐ°Ñ Ð¶Ðµ Ñ
оÑоÑаÑ, как обÑÑнаÑ
изоÑопиÑеÑÐºÐ°Ñ  -ÑиммеÑÑÐ¸Ñ Ð¸, во вÑÑком ÑлÑÑае, должна
вÑполнÑÑÑÑÑ Ð»ÑÑÑе, Ñем
-ÑиммеÑÑÐ¸Ñ Ð¸, во вÑÑком ÑлÑÑае, должна
вÑполнÑÑÑÑÑ Ð»ÑÑÑе, Ñем  -ÑиммеÑÑиÑ.
-ÑиммеÑÑиÑ.
Sergei B. Popov
2001-05-29






