SL в
Карткны дифракции Френеля на круглых диафраг-ме и экране (рис, 2 и 3) в общем случае трудны для анализа. Однако об их особенностях можно судить по освещ╦нности на осевой линии. За экраном па оси осве-
Г 7≈Г 7≈Т1
Теория Френеля полностью удовлетворяет требованиям практики, в первую очередь инструментальной оптики, однако она ограничена рамками эвристических принципов. Математически полное построение теории Френеля выполнил Г. Р. Кирхгоф (G. R. Kirchhoff; 1882), применив интегральное соотношение Гельмголь-
г) гхр (ikr) Vus ≈ " "
= J<K[
nxp
(6)
1,0
0,5
в
f(x)=
sin2 Г JZ
Рис- 5. Распределение интенсивности при дифракции па щели: а ≈ d≈1,01^2 ДХ; б≈ d=l,TlrRK; в ≈ дифракция Фраунго-фсра, х≈ 1/2kdsin(rtr). Пунктиром показано
распределение интенсивности, и-рос получилось Пы. по законам геометрической
оптики.
'V*Z1
0124 6 8 10
v ≈_
щсч шесть монотонно возрастает по мере удаления от экрана и стремится к V4 интенсивности падающего енота. Иа оси за круглой диафрагмой имеется бесконечное
Рис. в. Дифракция Фра-унгофера на прямоугольной диафрагме.
да связывающее поле в точке Р с его значением на произвольной поверхности, охватывающей Р\\ т ≈ расстояние до поверхности S. Кирхгоф показал, что если экран считать неизлучающим, т. е. поле и его нормальная производная на экране ≈ нули, то (6) принимает вид дифракц. интеграла (1). Однако в теории Кирхгофа не учитываются векторный характер световых волн и свойстьа самого материала экрана.
В строгих методах Д. с. рассматривается как вид рассеяния света, а математически ≈ как граничная задача рассеяния. Число таких задач, реш╦нных точно, невелико. Среди них реш╦нная первой А. Зоммвр-фельдом (A, Sommerfeld; 18li9) задача дифракции плоской волны на идеально проводящем клине. Решение этой задачи позволяет выяснить пределы применимости теории Френеля ≈ Кирхгофа и да╦т корректную ма-тем. основу представлениям Юнга. Иа этого решения следует, что свет проникает н область тени сильнее, чем предсказано (3). На открытой полуплоскости, дополняющей экран, там, где в теории Френеля ≈ Кирхгофа поле при нормальном падении считается заданным и постоянным, решение Зоммерфельда предсказывает сильные осцилляции при произвольных удалениях от края экрана. Зависимость поля от т вдали от края в области тени такая же, как соли бы край был линейным
источником иолны, т.е. u~i/V kr, что согласуется с представлениями Юнга. На самом деле, край не бесконечно тонкий источник, хотя и при приближении к нему плотность потока неограниченно раст╦т. По этой причине глазу, нккомодированиому на край, он кажется светящейся линией.
Развитие концепции излучающего края ≈ граничной дифрагированной волны ≈ и выяснение е╦ связи с теорией Френеля ≈ Кирхгофа выполнено Дж. А. Маджи (G. A. Maggi; 1888) и А. Рубиновичем (A, Rnbmowicz; 1917). Было показано, что интеграл Кирхгофа ≈ Фре-IICJIH по поверхности можно преставить двумя слагаемыми. Первому соответствует поле, описываемое законами геом. оптики. Второе ≈ интеграл по контуру края экрана (диафрагмы) ≈ описывает дифрагированное поле, источником к-рого служит этот край. Теория граничной дифрагированной волны правильно описывает
Фокальная плоскость
число мест, где интенсивность достигает интенсивности падающего света и в промежутках между ними ≈ бесконечное число мост с пулевой интенсивностью. Картина дифракции Фраупгофера на экране (диафрагме) представляет собой центральное яркое пятно, окруж╦нное системой томных и светлых колец, на долю к-рых проходится малая часть дифрагировавшего света.
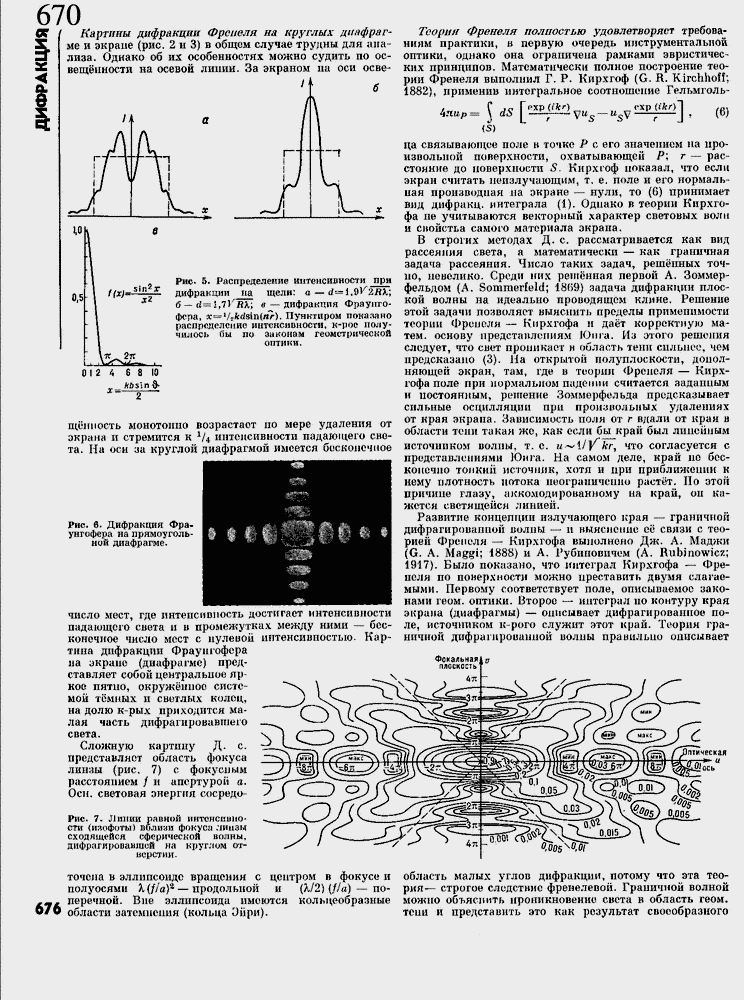
Сложную картину Д. с. представляет область фокуса линяы (рис, 7) с фокусным расстоянием / и апертурой а. Осн. световая энергия сосредо-
Рис. 7. Линии равной интенсивности (ивофоты) вблиаи фокуса линзы сходящейся сферической волны, дифрагировавшей на круглом отверстии.
точена в эллипсоиде вращения с центром в фокусе и область малых углов дифракции, потому что эта тео-
по л у осями K{f/a}* ≈ продольной и (К/ 2} (f/a) ≈ по- рля≈ строгое следствие френелевой. Граничной волной
._, перечной. Вне эллипсоида имеются кольцеобразные можно объяснить проникновение света в область геом.
О/О области затемнения (кольца Эйри). тени и представить это как результат своеобразного
птическая
и ось
")
}


