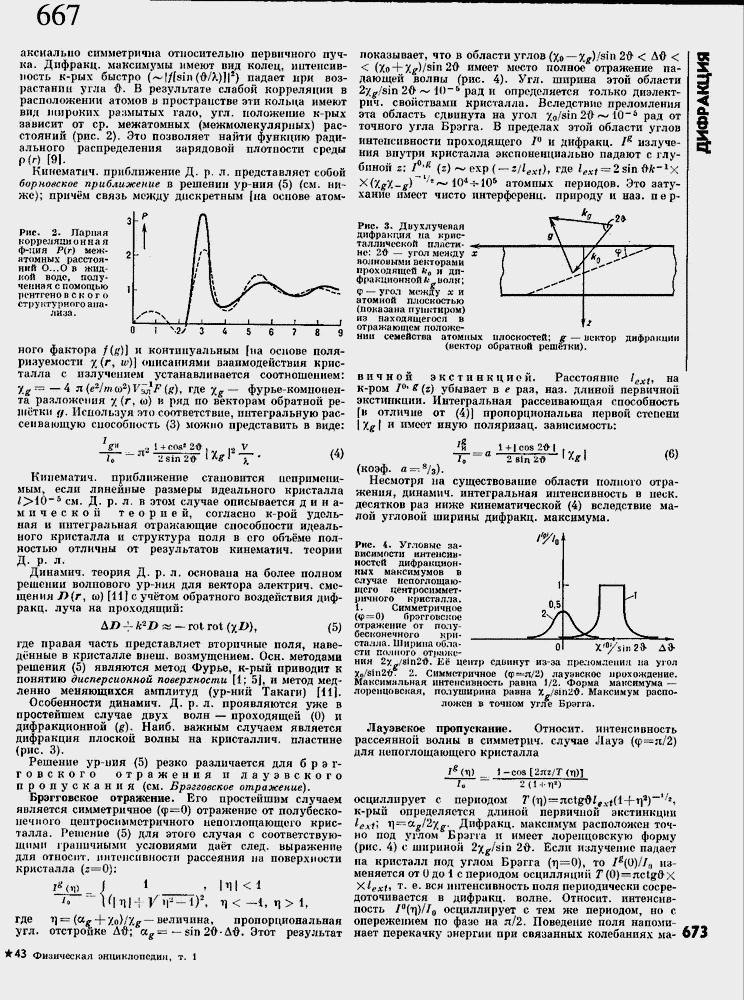
аксиально симметрична относительно первичного пучка. Дифракц, максимумы имеют вид колец, интенсивность к-рых быстро (~|/[sin (fr/X)]|2) падает при возрастании угла ft, В результате слабой корреляции в расположении атомов в пространстве эти кольца имеют вид широких ра:шытых галот угл. положение к-рых зависит от ср, межатомных (межмолекулярных) расстояний (рис. 2). Это позволяет найти функцию радиального распределения зарядовой плотности среды р(г) [9].
Кинематич. приближение Д. р. л, представляет собой борцовское приближение в решении ур-ния (5) (см. ниже); прич╦м связь между дискретным [на основе атом-
3 -
Рис. 2. Парная корреляционная ф-ция Р(г) меж-нтомных расстояний О-..О в жидкой воде, полученная с помощью уц-нтгенО в с к о г о структурного анализа .
ного фактора /(#)] и континуальным [па основе поляризуемости х (г, ы?)] описаниями взаимодействия кристалла с излучением устанавливается соотношением:
ymg = ≈4 л {е2/ю-гой)Уад /" (#), где х^-≈ фурье-Комнонен-та разложения х (г, to) в ряд по векторам обратной реш╦тки з/. Используя это соответствие, интегральную рассеивающую способность (3) можно представить в виде:
g" о 1 + cos* 2u , la ~Л" 2 sin 20 I
Кинеыатич. приближение становится неприменимым, если линейные размеры идеального кристалла />10~6 сы, Д. р. л. в этом случае описывается д и н а-м и ч е с к о ii теорией, согласно к-рой удельная и интегральная отражающие способности идеального кристалла и структура поля в его объ╦ме полностью отличны от результатов кинематич. теории Д. р. л.
Динамич. теория Д. р. л. основана на более полном решении волнового ур-ния для вектора электрич. смещения Г>(г, со) [11] с уч╦том обратного воздействия дифракц. луча на проходящий:
Д7> -;- ╧D KJ ≈ rot rot (x-Z>)» (5)
где правая часть представляет вторичные поля, наведенные в кристалле внеш. возмущением. Осн. методами решения (5) являются метод Фурье, к-рый приводит к понятию дисперсионной поверхности [1; 5], и метод медленно меняющихся амплитуд (ур-ний Такаги) [И].
Особенности динамич. Д, р. л, проявляются уже в простейшем случае двух волн ≈ проходящей (0) и дифракционной (g). Наиб, важным случаем является дифракция плоской волны на кристаллич. пластине {рис. 3).
Решение ур-иия (5) резко различается для б р э г-говского отражения и лауэвского пропускания (см. Брэгговское отражение).
Брэгговское отражение. Его простейшим случаем является симметричное (<р=0) отражение от полубеско-печного цептросимметричного непоглощающиго кристалла. Решение (5) для этого случая с соответствующими граничными условиями дает след, выражение для относит, интенсивности рассеяния па поверхности кристалла (г=0):

показывает, что в области углов (х0≈ х^)/зт2Ф < ДО < < fXo + X^)/s*n 20 имеет место полное отражение падающей волны (рис. 4). Угл. ширина этой области 2'/g/sm 20- ∙≈∙ 10 ~5 рад и определяется только диэлект-рич. свойствами кристалла. Вследствие преломления эта область сдвинута на угол у^/зт 2ft ~ Ш~5 рад от точного угла Брэгга, В пределах этой области углов
интенсивности проходящего /° и дифракц. Is излучения внутри кристалла экспоненциально падают с глубиной z\\ /°'я (z) ~ ехр ( ≈ zjlext), где lext = 2sm^k-lx
Х(Х^Х-^} 'Е~104^-105 атомных периодов. Это затухание имеет чисто тштерфсренц. природу и наз. пер-
Рис. 3. Дьухдучепая дифракция на кристаллической ПЛЙСТИ- -не: 2# ≈ угол между х волновыми векторами проходящей fcn и ди-фракционнойА: волк;
Ф - ≈ угол между х и атомной плоскостью (показана гтуш.-тиром) из находящегося в отражающем положении семейства атомных плоскостей;
V
Л,
g
(вектор обратной реш╦тки),
дифракции
вичной экстинкциой. Расстояние 1вх^ на к-ром /Oifi"(z) убывает в е рав, наз. длиной первичной экстшгкции. Интегральная рассеивающая способность [в отличив от (4)] пропорциональна первой степени | и имеет иную поляризац. зависимость:
и
-а 1+|С05^' [у 1 (К) ~«-а 2 sin 2^ 1ЭС*1 W
(коэф. я~8/3).
Несмотря на существование области полного отражения, динамич. интегральная интенсивность в неск. десятков раз ниже кинематической (4) вследствие малой угловой ширины дифракц. максимума.
Рис. 4. Угловые зависимости интенсии-ностсй дифракционных максимумов в случае нспоглощаю-щсго центросиммет-р ичного кристалла. 1. Симметричное (Ф ≈ 0) Орэггоиское отражение от гтолу-беснонечного кристалла. Ширина, области полного отраже-
2^ ДЭ-
ния 2>∙ /$ii\\2-&, К╦ центр сдвинут из-за преломления на угол
X0/sin2-&. 2. Симметричное (ср=я/2) лауавскос прохождение. Максимальная интенсивность равна 1/2. Форма максимума ≈ лоренцовсная, полуширина равна % /sin'A-d1. Максимум расположен в точном угле Брэгга.
Лауэвское пропускание. Относит, интенсивность рассеянной волны в симметрии, случае Лауэ (ф≈л/2) для шэпоглощающбго кристалла
j-cos [2яг/Г<тр] 2 (1ч-Т1в)
Т(П) =
О2,
< ≈1,
_^f__^
§
а
i
где
т] ≈ (ce^ + Xp)/Xg.≈неличина» пропорциональная угл. отстройке A-ft; &g= ≈ sin 20- ДО. Этот результат
Л,
осциллирует с периодом к-рый определяется длиной первичной экстинкции ^л-fi т] ≈а^/2х^. Дифракц. максимум расположен точно под углом Брэгга и имеет лореицовскую форму (рис. 4) с шириной 2x£/sin Зб1. Если иалучепие падает
на кристалл под углом Брэгга (т]=0), то /╦(0)//0 изменяется от U до 1 с периодом осцилляции Г(0)=яс1^х X/^jcb T' е- вся интенсивность поля периодически сосредоточивается в дифракц. волне. Относит, интенсивность /а(т])//0 осциллирует с тем же периодом, но с опережением по фаае на л/2. Поведение поля напоми- .__ нает перекачку энергии при связанных колебаниях ма- 673
Ж 43 Физическая энциклопсдил, т, 1
")
}



