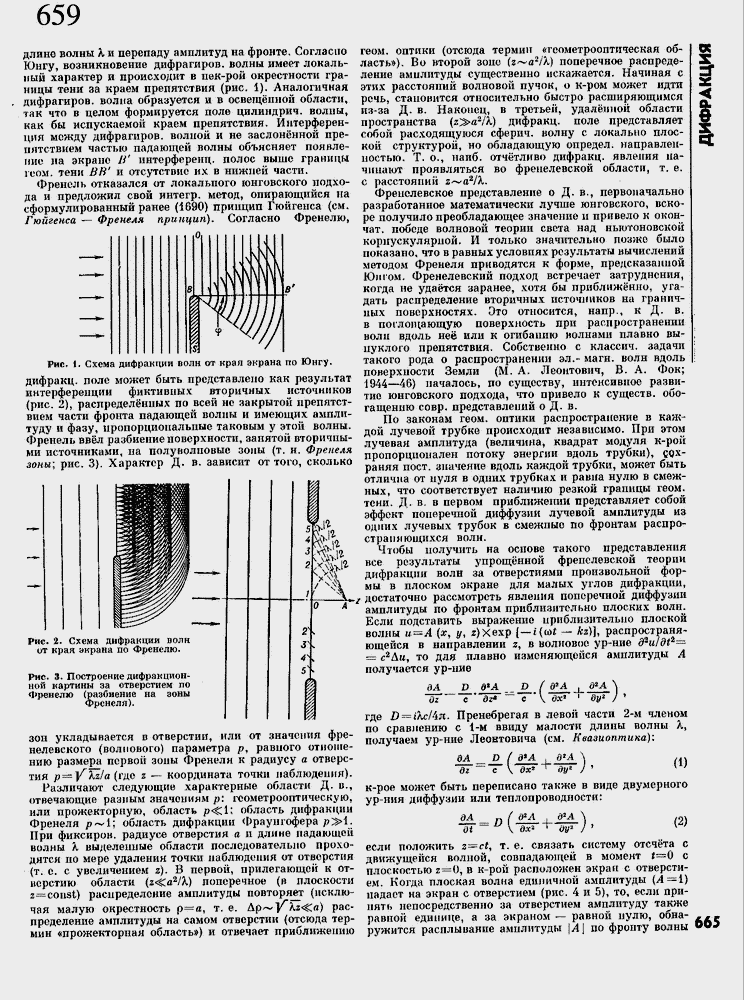
длине волны К и перепаду амплитуд на фронте. Согласно Юнгу, возникновение дифрагиров. волны имеет локальный характер и происходит в пек-рой окрестности границы тени за краем препятствия (рис. 1), Аналогичная дифрагиров. волна образуется и в освещ╦нной области, так что в целом формируется поле цилиндрич. волны, как бы испускаемой краем препятствия. Интерференция между дифрагиров, волной и не заслон╦нной препятствием частью падающей волны объясняет появлении на экране В' интерференц. полос выше границы юом. тени ВВ' и отсутствие их в нижней части.
Френель отказался от локального юнговского подхода и предложил свой интегр. метод, опирающийся на сформулированный ранее (1690) принцип Гюйгенса (см, Гюйгенса ≈ Френеля принцип). Согласно Френелю,
О
Рис. 1, Схема дифракции волн от края экрана по Юнгу.
дифракц, поле может быть представлено как результат интерференции фиктивных вторичных источников (рис. 2), распредел╦нных по всей не закрытой препятствием части фронта падающей волны и имеющих амплитуду и фазу, пропорциональные таковым у этой волны, Френель вв╦л разбиение поверхности, занятой вторичными источниками, на полуволповые зоны (т. н, Френеля зоны] рис. 3). Характер Д. в. зависит от того, сколько
Рис. 2. Схема дифракции волн от края экрана по Френелю.
Рие. а. Построение дифракционной картины за отверстием по Френелю (разбиение на зоны Френеля).
зон укладывается в отверстии, или от значения фре-нелевского (волнового) параметра р, равного отношению размера первой зоны Френеля к радиусу а отверстия р ≈ У"Яд/я (гдо г ≈ координата точки наблюдения). Различают следующие характерные области Д. в., отвечающие разным значениям р\\ геометрооптическую, или прожекторную, область p-cl; область дифракции Френеля р~1; область дифракции Фраунгофера р>1. При фиксирон. радиусе отверстия а и длине падающей волны А, выделенные области последовательно проходятся по мере удаления точки наблюдения от отверстия (т. с. с увеличением z). В первой, прилегающей к отверстию области (г<О2/Я) поперечное (н плоскости 2=coiist) распределение амплитуды повторяет (исключая малую окрестность р≈а, т. е. Др~У Я-г<с«) распределение амплитуды на самом отверстии (отсюда термин «прожекторная область») и отвечает приближению
геом. оптики (отсюда термин «гсометрооптическая область»). Во второй зоне (з-≈-а2А) поперечное распределение амплитуды существенно искажается. Начиная с этих расстояний волновой пучок, о к-ром может идти рочь, становится относительно быстро расширяющимся из-за Д. в. Наконец, в третьей, удал╦нной области пространства (г^>я2/Я,) дифракц. поле представляет собой расходящуюся сферич. волну с локально плоской структурой, но обладающую определ. направленностью. Т. о., наиб, отч╦тливо дифракц. явления начинают проявляться во фреиелевской области, т. е. с расстояний я~а2А.
Френслевское представление о Д. в., первоначально разработанное математически лучше юнговского, вскоре получило преобладающее значение и привело к окончат, победе волновой теории света над ньютоновской корпускулярной. И только значительно позже было показано, что в равных условиях результаты вычислений методом Френеля приводятся к форме, предсказанной Юпгом. Френелевский подход встречает затруднения, когда не уда╦тся заранее, хотя бы приближ╦нно, угадать распределение вторичных источников на граничных поверхностях. Это относится, напр., к Д. в. в поглощающую поверхность при распространении воля вдоль не╦ или к огибанию нолыами плавно выпуклого препятствия. Собственно с классич. задачи такого рода о распространении эл.- магн. волн вдоль поверхности Земли (М. А. Леоитович, В. А. Фок; 1944≈46) началось, по существу, интенсивное развитие юнговского подхода, что привело к существ, обогащению совр, представлений о Д. в.
По законам геом. оптики распространение в каждой лучевой трубке происходит независимо. При этом лучевая амплитуда (величина, квадрат модуля к-рой пропорционален потоку энергии вдоль трубки), сохраняя пост, значение вдоль каждой трубки, может быть отлична от пуля в одних трубках и равна нулю в смежных, что соответствует наличию резкой границы геом. тени. Д. в. в первом приближении представляет собой эффект поперечной диффузии лучевой амплитуды из одних лучевых трубок в смежные по фронтам распространяющихся волн.
Чтобы получить на основе такого представления все результаты упрощ╦нной френелевской теории дифракции волн за отверстиями произвольной формы в плоском экране для малых углов дифракции, достаточно рассмотреть явления поперечной диффузии амплитуды по фронтам приблизительно плоских волн. Если подставить выражение приблизительно плоской волны ы=Л (#, у, z)Xexp [ ≈ i(idt ≈ ftz)], распространяющейся в направлении z, в волновое ур-ние с*2и/с^2= = с2Ды, то для плавно изменяющейся амплитуды А получается ур-ние
р с
dz
дт*
где = icn. Пренебрегая в левой части 2-м членом по сравнению с 1-м ввиду малости длины волны Я,, получаем ур-ние Леоктовича (см. Квазиоптика):
дА дг
D С
, ~Г
д*А_ ду*
к-рое может быть переписано также в виде двумерного ур-ния диффузии или теплопроводности:
дА
= D
(2)
если положить z=ct, т. е. связать систему отсч╦та с движущейся волной, совпадающей в момент t=0 с плоскостью 2≈0, в к-рой расположен экран с отверстием. Когда плоская волна единичной амплитуды (А = 1) падает на экран с отверстием (рис. 4 и 5), то, если при-пять непосредственно за отверстием амплитуду также равной единице, а за экраном ≈ равной пулю, обна- , , -ружится расплыианпе амплитуды А \\ по фронту волны &0J
")
}


