чает начальному (*/≈>∙ ≈ оо), другое ≈ конечному -»∙ оо) моментам времени.
А. р. Л$, в является матричным элементом матрицы (оператора) рассеяния Т:
(1)
(2)
к- рая связана с 5- матрице]! соотношением и имеет вид
Здесь //-- //о ≈ У"- #rrf 1" ≈ полный гамильтониан системы, .//п и V ≈ свободный гамильтониан и взаимо-
действие, отвечающее состоянию системы в момент
времени 2; (HQ, V ≈ соответствующие величины в конечный момент промен u tfa '/Ь> /а ≈ собств. ф-ции в
состоянии непрерывного спектра свободных гамильто-
нианов #о и ∙'Ль ^ц ≈ собств. значение энергии, отвечающее состоянию у.д,
Благодаря сохранению импульса амплитуда АЬ.Ч может быть записаЕ1а в форме
где pf(pf ≈ тр╦хмерны импульс системы начального (конечного) состояния, д (х) ≈ дельта-функция Дирака. Часто термин «А. р.» применяется к величине ^ь,а. В низшем приближении по взаимодействию А. р. да╦тся матричным элементом от потенциала взаимодействия V, что соответствует борцовскому приближению. Для простейшего случая рассеяния нерелятинистской бесспиновой частицы в сферически симметричном потенциале V (г) {г ≈ расстояние до рассеивающего центра) А, р. имеет вид Tbi0 ≈ f(Q,z) и характеризуется углом рассеяния 9 и энергией Б (здесь & ≈ pz/2rn, p = \\pt\\--= pj\\i cos Q=Pipfjp2i m ≈ масса частицы). A. p. / (0, s) определяет асимптотику на больших расстояниях г точной волновой ф-ции системы ty (r) (к-рая является собств. ф-цией гамильтониана Я), а именно при направлении начального импульса вдоль оси г:
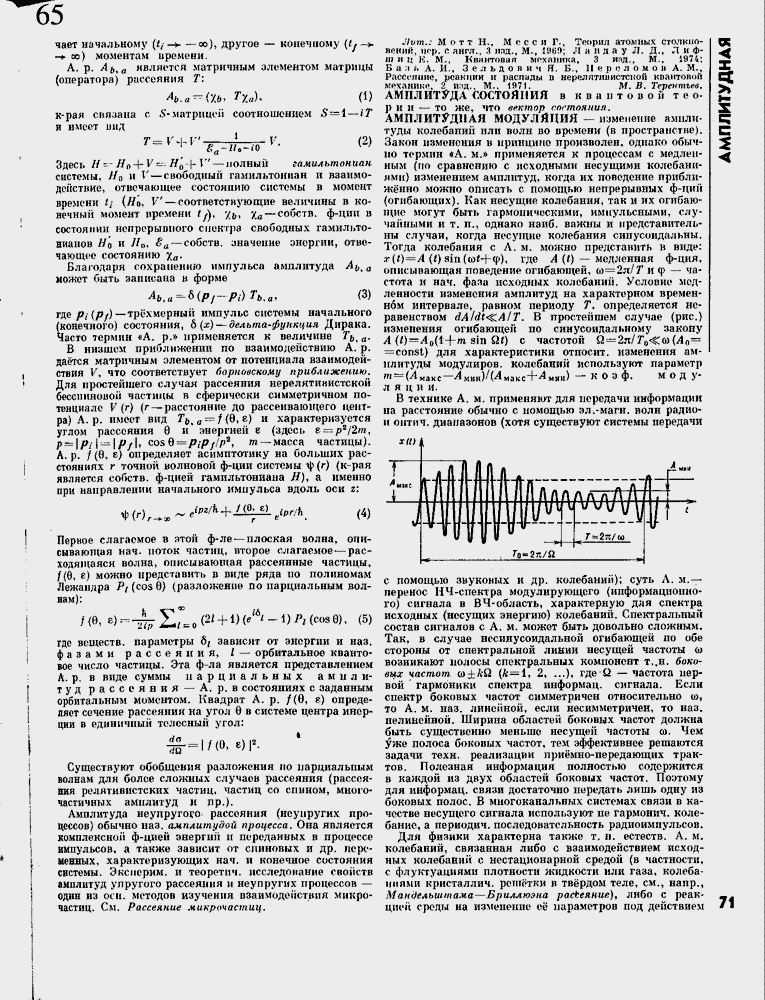
Лут.: М о т т Н,, М с с с и Г., Теория атомных столкновений, игр. с англ., З'ипд., М., 196Я; Л а и н а у Л. Д., Л и ф-П1 и ц К. М., Квянтовгш механика, 3 ияд., М., 1974; Б a ;t г, А. И., 3 е л ь д о в и ч Я, В., II е р о л о м о в А. М., Рассеяние, реакции и распады в нерелятшшстской квантовой механиь-п, 2 и:щ., М., 1971. М, В, Тереюпъив. АМПЛИТУДА СОСТОЯНИЯ в квантовой те о-Р И и ≈ то же, что вектор состояния. АМПЛИТУДНАЯ МОДУЛЯЦИЯ ≈ изменение амшш-туды колебаний или волн во времени (в пространстве). Закон изменения в принципе произволен, однако обычно термин «А, м.» применяется к процессам с медленным (по сравнению с исходными несущими колебаниями) изменением амплитуд, когда их поведение приближ╦нно можно описать с помощью непрерывных ф-цшг (огибающих). Как несущие колебания, так и их огибающие могут быть гармоническими, импульсными, случайными и т. п., однако наиб, важны и представительны случаи, когда несущие колебания синусоидальны. Тогда колебания с А, м. можно представить в виде: ?(t)=A (t) зт(юг≈ф), где A (t) ≈ медленная ф-ция, описывающая поведение огибающей, ш=2л/?1 и ф ≈ частота и нач. фала исходных колебаний. Условие медленности изменения амплитуд на характерном временном интервале, равном периоду Т1, определяется неравенством dA/dt<^A/T. В простейшем случае (рис.) изменения огибающей по синусоидальному закону A (t)=AQ(l-\\-m sin Ш) с частотой Q ≈2л/7т└<§:й>(Ло= =const) для характеристики относит, изменения амплитуды модулиров. колебаний используют параметр w ≈(Лмакс≈Лмвн)/(Лмакс+4МЯ11) ≈ к О э ф. моду-л я ц и и,
В технике А. м. применяют для передачи информации па расстояние обычно с помощью эл.-магн. волн радио-it онтич. диапазонов (хотя существуют системы передачи
МИН
-X
Первое слагаемое в этой ф-ле ≈ плоская волна, описывающая нач. поток частиц, второе слагаемое ≈ расходящаяся волна, описывающая рассеянные частицы, /(0, е) можно представить в виде ряда по полиномам Лежандра P/(cos6) (разложение по парциальным волнам):
(5)
где веществ, параметры бг зависят от энергии и наз. фазами рассеяния, I ≈ орбитальное квантовое число частицы. Эта ф-ла является представлением А. р. в виде суммы парциальных амплитуд рассеяния ≈ А, р. в состояниях с заданным Орбитальным моментом. Квадрат А. р, /(0, е) определяет сечение рассеяния на угол 6 в системе центра инерции в единичный телесный угол:
Существуют обобщения разложения по парциальным волнам для более сложных случаев рассеяния (рассеяния релятивистских частиц, частиц со спином, много-частичных амплитуд и пр.),
Амплитуда неулругого. рассеяния (неупругих процессов) обычно наз, амплитудой процесса. Она является комплексной ф-цией энергий и переданных в процессе импульсов, а также зависит от спиновых и др. переменных, характеризующих нач. и конечное состояния системы. Эксмерим. и теоретнч. исследование свойств амплитуд упругого рассеяния и неупругих процессов ≈ один из осп. методов изучения взаимодействия микрочастиц. См. Рассеяние макрочастиц.
с помощью звуковых и др. колебаний); суть Л. м.≈ перенос НЧ-спектра модулирующего (информационного) сигнала в ВЧ-область, характерную для спектра исходных (несущих энергию) колебаний. Спектральный состав сигналов с А. м. может быть довольно сложным. Так, в случае нссинусоидальной огибающей по обе стороны от спектральной линии несущей частоты <D возникают полосы спектральных компонент т.,н. боковых частот со^А:Й (& = 1, 2, ...), где-Q ≈ частота первой гармоники спектра информац. сигнала. Если спектр боковых частот симметричен относительно to, то А. м. наз. линейной, если несимметричен, то наз. нелинейной. Ширина областей боковых частот должна быть существенно меньше несущей частоты со. Чем уже полоса боковых частот, тем эффективнее решаются задачи техн. реализации прие'мно-передающих трактов. Полезная информация полностью содержится в каждой из двух областей боковых частот. Поэтому для информац. связи достаточно передать лишь одну из боковых полос. В многоканальных системах связи в качестве несущего сигнала используют не гармонич. колебание, а периодич. последовательность радиоимпульсов. Для физики характерна также т. а. естеств. А. м. колебаний, связанная либо с взаимодействием исходных колебаний с нестационарной средой (в частности, с флуктуацнями плотности жидкости или газа, колебаниями кристаллич. решетки в тв╦рдом теле, см.т напр., Мандельштама≈Бриллюэиа рассеяние), либо с реак^ циок среды на изменение е╦ параметров под действием
X
с;
с
71
")
}


