1tom - 0520.htm
567
где ./V ≈ число элементарных ячеек, V ≈ объ╦м тела, ∙V ≈ число частиц в элементарной ячейке.
–î. —Ç. —Ö–∞—Ä–∞–∫—Ç–µ—Ä–∏–∑—É–µ—Ç –º–Ω. —Å–≤–æ–π—Å—Ç–≤–∞ —Ç–≤‚ﶗĖ¥—ã—Ö —Ç–µ–ª: —Ç–µ–ø–ª–æ‚ﶖº–∫–æ—Å—Ç—å, —Ç–µ–ø–ª–æ- –∏ —ç–ª–µ–∫—Ç—Ä–æ–ø—Ä–æ–≤–æ–¥–Ω–æ—Å—Ç—å, —É–ø—Ä—É–≥–∏–µ —Å–≤–æ–π—Å—Ç–≤–∞, —É–ø—à—Ä–µ–Ω–∏–µ –ª–∏–Ω–∏–∏ —Ä–µ–Ω—Ç–≥. —Å–ø–µ–∫—Ç—Ä–æ–≤ –∏ —Ç. –ø. –î. —Ç. —è–≤–ª—è–µ—Ç—Å—è —Ö–∞—Ä–∞–∫—Ç–µ—Ä–Ω—ã–º –º–∞—Å—à—Ç–∞–±–æ–º, —Ä–∞–∑–¥–µ–ª—è—é—â–∏–º –æ–±–ª–∞—Å—Ç—å –≤—ã—Å–æ–∫–∏—Ö —Ç–µ–º–ø-—Ä (7*3>9–æ)—Ç –≤ –∫-—Ä–æ–π –∫–æ–ª–µ–±–∞–Ω–∏—è –∫—Ä–∏-—Å—Ç–∞–ª–ª–∏—á. —Ä–µ—à‚ﶗǖ∫–∏ –º–æ–∂–Ω–æ –æ–ø–∏—Å—ã–≤–∞—Ç—å –∫–ª–∞—Å—Å–∏—á. —Ç–µ–æ—Ä–∏–µ–π –∏ –≥–¥–µ, –≤ —á–∞—Å—Ç–Ω–æ—Å—Ç–∏, —Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤ –î—é–ª–æ–Ω–≥–∞ –∏ –ü—Ç–∏ –∑–∞–∫–æ–Ω, –∏ –æ–±–ª–∞—Å—Ç—å –Ω–∏–∑–∫–∏—Ö —Ç–µ–º–ø-—Ä (7^6–æ)» –≥–¥–µ —Å—Ç–∞–Ω–æ–≤—è—Ç—Å—è —Å—É—â–µ—Å—Ç–≤–µ–Ω–Ω—ã–º–∏ –∫–≤–∞–Ω—Ç–æ–≤–æ–º–µ—Ö–∞–Ω–∏—á. —ç—Ñ—Ñ–µ–∫—Ç—ã.
Д. т. обычно находят пут╦м поагонки наблюдаемых значений уд. тепло╦мкости к ф-ле, даваемой теорией Дебая, в точке, где величина тепло╦мкости составляет половину от значения, соответствующего закону Дюлонга и Пти. Полученные таким пут╦м значения Д. т. для нек-рых элементов приведены в табл. 1.
Табл. 1. ≈Температура Дебая для рваных веществ
|
|
|
|
|
|
|
|
|
|
|
|
|
–≠–ª–µ–º–µ–Ω—Ç
|
*
|
–≠–ª–µ–º–µ–Ω—Ç
|
–Ø
|
–≠–ª–µ–º–µ–Ω—Ç
|
–∏
|
–≠–ª–µ–º–µ–Ω—Ç
|
–ö
|
|
|
|
|
–∞
|
|
*‚àô
–ò
|
|
n
|
|
fl
|
|
|
|
|
CD
|
|
CD
|
|
–æ
|
|
X-
|
|
|
|
Li
|
400
|
Sn
|
|
In
|
|
Pd
|
|
|
|
|
Na
|
|
(—Å–µ—Ä–æ–µ)
|
|
–¢1
|
|
Cd
|
|
|
|
|
–ö
|
|
(–±–µ–ª–æ–µ)
|
|
–° (–∞–ª–º–∞–∑)
|
I860
|
Hg
|
|
|
|
|
Be
|
|
–ê–∑
|
|
Si
|
|
Cr
|
|
|
|
|
Mg
|
|
Bi
|
|
Ge
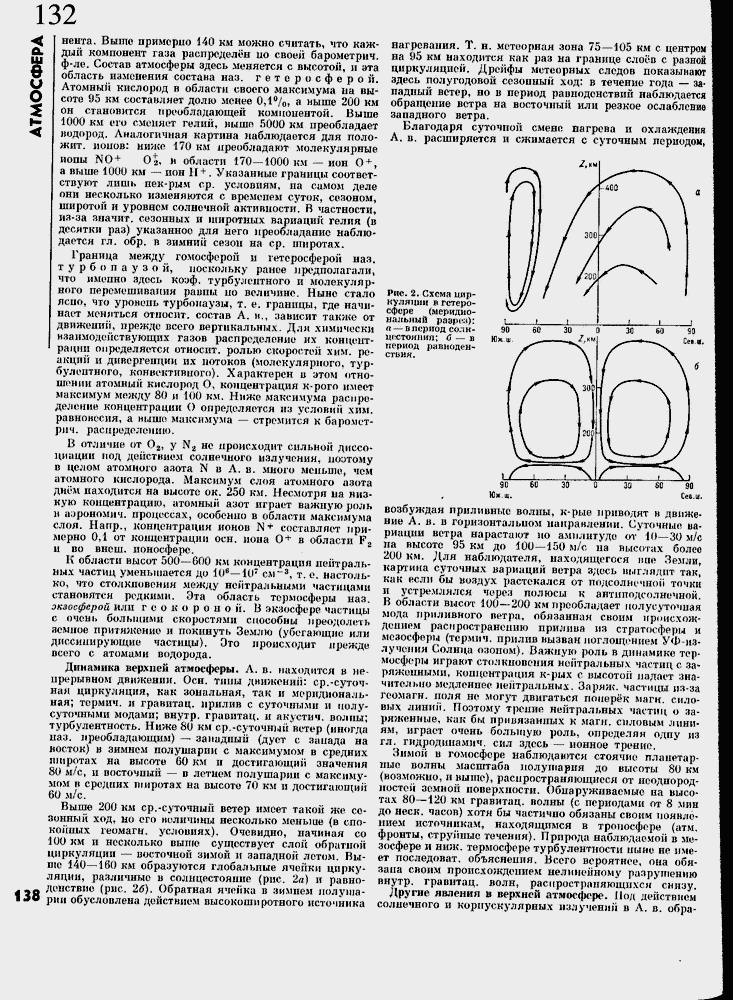
|
3(30
|
Mo
|
|
|
|
|
–°–∞
|
|
–ê–≥
|
|
W
|
|
Pt
|
|
|
|
|
–í
|
1250
|
–°–∏
|
|
Fe
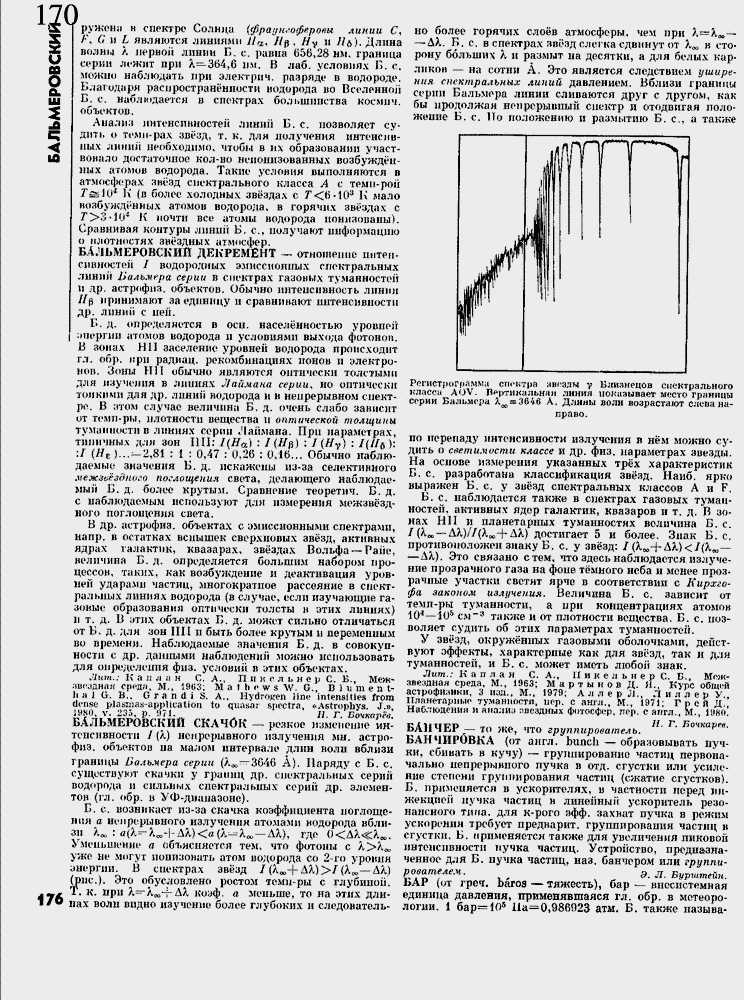
|
|
La
|
|
|
|
|
–ê\\
|
394
|
Ag
|
|
Co
|
|
Gd
|
|
|
|
|
Ga
|
240
|
–ê–∏
|
|
Mi
|
|
Pr
|
|
|
|
|
|
|
Zn
|
2,44
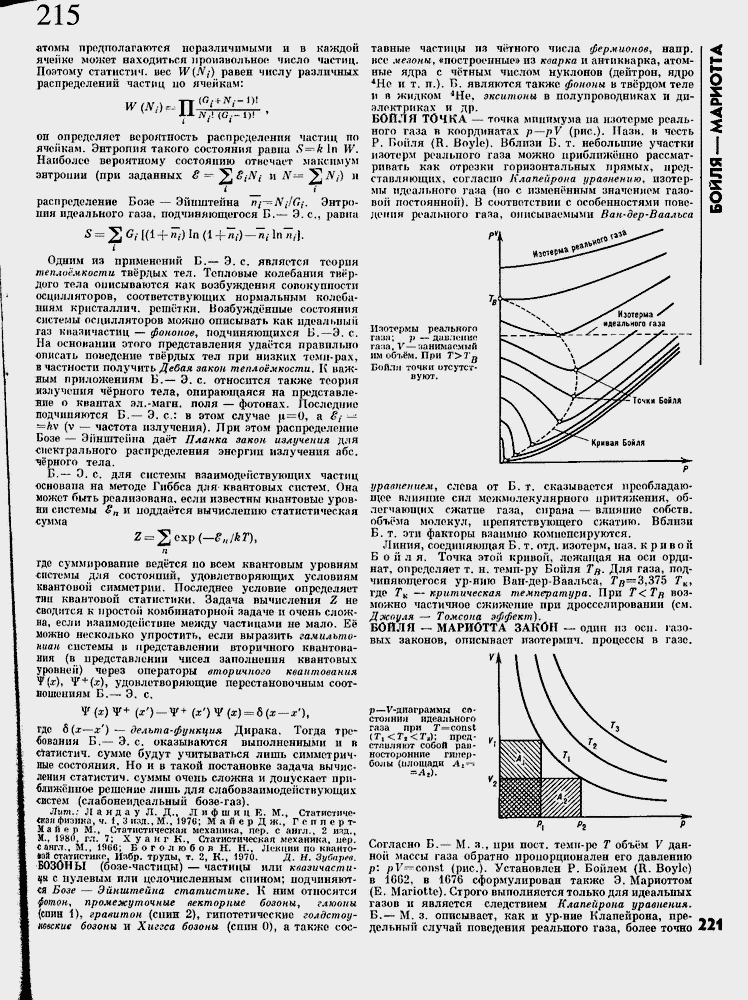
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–æ—Ç–≤–µ—Ç—Å—Ç–≤—É–µ—Ç –æ—Ç–¥. –Ω–æ—Ä–º–∞–ª—å–Ω–æ–º—É –∫–æ–ª–µ–±–∞–Ω–∏—é —Å–∏—Å—Ç–µ–º—ã (—Å–º. –ö–æ–ª–µ–±–∞–Ω–∏—è –∫—Ä–∏—Å—Ç–∞–ª–ª–∏—á–µ—Å–∫–æ–π —Ä–µ—à‚ﶗǖ∫–∏). –í—ã—á–∏—Å–ª–µ–Ω–∏–µ —Å—Ç–∞—Ç–∏—Å—Ç–∏—á–µ—Å–∫–æ–π —Å—É–º–º—ã –∏, —Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª—å–Ω–æ, —Ç–µ—Ä–º–æ–¥–∏–Ω–∞–º–∏—á. —Ñ-—Ü–∏–π —Ç–∞–∫–æ–π —Å–∏—Å—Ç–µ–º—ã –≤ –æ–±—â–µ–º –≤–∏–¥–µ –Ω–µ–≤–æ–∑–º–æ–∂–Ω–æ, —Ç. –∫. —Ä–µ–∑—É–ª—å—Ç–∞—Ç —Å—É—â–µ—Å—Ç–≤–µ–Ω–Ω–æ –∑–∞–≤–∏—Å–∏—Ç –æ—Ç –∫–æ–Ω–∫—Ä–µ—Ç–Ω–æ–≥–æ —Ä–∞—Å–ø—Ä–µ–¥–µ–ª–µ–Ω–∏—è —á–∞—Å—Ç–æ—Ç –ø–æ —Å–ø–µ–∫—Ç—Ä—É –∫–æ–ª–µ–±–∞–Ω–∏–π —Ç–≤‚ﶗĖ¥–æ–≥–æ —Ç–µ–ª–∞, —Ç.–µ. –æ—Ç –ø–ª–æ—Ç–Ω–æ—Å—Ç–∏ –∫–æ–ª–µ–±–∞—Ç. —Å–æ—Å—Ç–æ—è–Ω–∏–π #(—à), –≥–¥–µ –π> ‚âà —á–∞—Å—Ç–æ—Ç–∞ –∫–æ–ª–µ–±–∞–Ω–∏–π. –û–¥–Ω–∞–∫–æ –≤ –ø—Ä–µ–¥–µ–ª—å–Ω–æ–º —Å–ª—É—á–∞–µ –Ω–∏–∑–∫–∏—Ö —Ç–µ–º–ø-—Ä –∑–∞–¥–∞—á–∞ —É–ø—Ä–æ—â–∞–µ—Ç—Å—è, —Ç. –∫. –≤–æ–∑–±—É–∂–¥–∞—é—Ç—Å—è —Ç–æ–ª—å–∫–æ –∫–æ–ª–µ–±–∞–Ω–∏—è –Ω–∏–∑–∫–∏—Ö —á–∞—Å—Ç–æ—Ç (—é~£–ì/–î, –¢ ‚âà –∞–±—Å. —Ç–µ–º–ø-pa). –û–Ω–∏ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª—è—é—Ç —Å–æ–±–æ–π –∑–≤—É–∫–æ–≤—ã–µ –≤–æ–ª–Ω—ã —Å –ª–∏–Ω–µ–π–Ω—ã–º –∑–∞–∫–æ–Ω–æ–º –¥–∏—Å–ø–µ—Ä—Å–∏–∏; o>=qA; –¥–ª—è –ø—Ä–æ–¥–æ–ª—å–Ω—ã—Ö –∏ oo~ct& –¥–ª—è –ø–æ–ø–µ—Ä–µ—á–Ω—ã—Ö –≤–æ–ª–Ω (cf nct ‚âà –ø—Ä–æ–¥–æ–ª—å–Ω–∞—è –∏ –ø–æ–ø–µ—Ä–µ—á–Ω–∞—è —Å–∫–æ—Ä–æ—Å—Ç–∏ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏—è –≤–æ–ª–Ω, –ê ‚âà –≤–æ–ª–Ω–æ–≤–æ–µ —á–∏—Å–ª–æ). –¢. –æ., –ø—Ä–∏ –Ω–∏–∑–∫–∏—Ö —Ç–µ–º–ø-pax –¥–∏—Å–∫—Ä–µ—Ç–Ω–∞—è —Å—Ç—Ä—É–∫—Ç—É—Ä–∞ –∫—Ä–∏—Å—Ç–∞–ª–ª–∏—á. —Ä–µ—à‚ﶗǖ∫–∏ –Ω–µ –ø—Ä–æ—è–≤–ª—è–µ—Ç—Å—è. –ü–ª–æ—Ç–Ω–æ—Å—Ç—å –∫–æ–ª–µ–±–∞—Ç. —Å–æ—Å—Ç–æ—è–Ω–∏–π, —Ç. –µ. —á–∏—Å–ª–æ —Å–æ–±—Å—Ç–≤–µ–Ω–Ω—ã—Ö –∫–æ–ª–µ–±–∞–Ω–∏–π –≤ –∏–Ω—Ç–µ—Ä–≤–∞–ª–µ —á–∞—Å—Ç–æ—Ç –æ—Ç —à –¥–æ co-^-dco –≤ —Å–ø–µ–∫—Ç—Ä–µ –∑–≤—É–∫–æ–≤—ã—Ö –≤–æ–ª–Ω—Ç —Ä–∞–≤–Ω–∞:
, * , ттЗы* dtt) /jx g (0)) АО = V≈≈-=s- , (1)
Для сложных кристаллич. реш╦ток вводят т, н. ха-рактеристич. Д. т., к-рая подбирается так, чтобы соответствующие ф-лы правильно описывали наблюдаемые температурные зависимости, напр, тепло╦мкости. При этом характеристич. Д. т. сама является ф-цией темп-ры. Эксперям. или теоретич. данные по тепло╦мкости представляются в виде графика Qo(Cv) от Т. Значение характеристич. Д. т. при 5Г=0 можно вычислить теоретически, зная упругие постоянные реш╦тки. Сравнение Д. т., полученных по измерению Су и вычисленных из упругих постоянных (табл. 2), позволяет получить информацию об особенностях межатомных связей и ди-намич. свойствах реш╦тки кристалла.
Табл. 2, ≈Значения характеристической температуры Дебая при Т^О К
|
|
|
|
|
|
|
|
|
|
|
–í–Ý–©–°-
|
eD (–°—É),
|
eD<ynp.x
|
–í–µ—â–µ-
|
eD(Cv).
|
6D (–£–ø—Ä.),
|
|
|
|
–°–¢–í–û
|
–∫
|
–∫
|
—Å—Ç–≤–æ
|
–ö
|
–ö
|
|
|
|
–°–∏
|
345,2
|
344,4
|
Mg
|
404,6
|
385,8
|
|
|
|
Ag
|
226,0
|
226.4
|
Zn
|
305,5
|
|
|
|
|
–ê–∏
|
164,7
|
161,1
|
Ge
|
374,0
|
≈
|
|
|
|
LIF
|
740,0
|
734,1
|
Si
|
674,8
|
≈ ≈
|
|
|
|
|
|
|
|
|
|
|
где V ≈ объ╦м тела, с ≈ усредненная скорость звука, к-рая для изотропного тела определяется соотношением:
3_ __2 | __1 /–ø\\
–¢–ì^-^+^–ì' <2>
1* 1
‚àô -t
–í —Å–ª—É—á–∞–µ –∞–Ω–∏–∑–æ—Ç—Ä–æ–ø–Ω—ã—Ö –∫—Ä–∏—Å—Ç–∞–ª–ª–æ–≤ –∑–∞–∫–æ–Ω —É—Å—Ä–µ–¥–Ω–µ–Ω–∏—è –∏–∑–º–µ–Ω—è–µ—Ç—Å—è, –æ–Ω —Ç—Ä–µ–±—É–µ—Ç —Ä–µ—à–µ–Ω–∏—è –∑–∞–¥–∞—á–∏ —Ç–µ–æ—Ä–∏–∏ —É–ø—Ä—É–≥–æ—Å—Ç–∏ –æ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏–∏ –∑–≤—É–∫–∞ –≤ –∫—Ä–∏—Å—Ç–∞–ª–ª–µ –¥–∞–Ω–Ω–æ–π —Å–∏–º–º–µ—Ç—Ä–∏–∏. –ó–∞–≤–∏—Å–∏–º–æ—Å—Ç—å –∂–µ –ø–ª–æ—Ç–Ω–æ—Å—Ç–∏ g –æ—Ç —á–∞—Å—Ç–æ—Ç—ã (1) —Å–æ—Ö—Ä–∞–Ω—è–µ—Ç—Å—è,
В предельном случае высоких темп-р где а ≈ постоянная реш╦тки) возбуждены все 3^Vv колебат. степеней свободы и на каждую приходится энергия kT (закон равнораспределения). В обоих предельных случаях статистич, сумма и термодинамич. ф-ции кристаллич. реш╦тки могут быть вычислены.
–î. —Ç. –ø—Ä–µ–¥—Å—Ç–∞–≤–ª—è–µ—Ç —Å–æ–±–æ–π –∏–Ω—Ç–µ—Ä–ø–æ–ª—è—Ü–∏—é –º–µ–∂–¥—É —ç—Ç–∏–º–∏ –ø—Ä–µ–¥–µ–ª—å–Ω—ã–º–∏ —Å–ª—É—á–∞—è–º–∏. –û–Ω–∞ –ø—Ä–µ–¥–ø–æ–ª–∞–≥–∞–µ—Ç, —á—Ç–æ –¥–ª—è –≤—Å–µ—Ö –ó–õ–ß> –Ω–æ—Ä–º–∞–ª—å–Ω—ã—Ö –∫–æ–ª–µ–±–∞–Ω–∏–π –∏–º–µ–µ—Ç –º–µ—Å—Ç–æ –ª–∏–Ω–µ–π–Ω—ã–π –∑–∞–∫–æ–Ω –¥–∏—Å–ø–µ—Ä—Å–∏–∏ –∏ –ø–ª–æ—Ç–Ω–æ—Å—Ç—å –∫–æ–ª–µ–±–∞—Ç. —Å–æ—Å—Ç–æ—è–Ω–∏–π –æ–ø–∏—Å—ã–≤–∞–µ—Ç—Å—è —Ñ-–ª–æ–π (1), —á—Ç–æ –≤ –¥–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ—Å—Ç–∏ —Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–æ –ª–∏—à—å –¥–ª—è –º–∞–ª—ã—Ö —á–∞—Å—Ç–æ—Ç. –°–ø–µ–∫—Ç—Ä –∫–æ–ª–µ–±–∞–Ω–∏–π –Ω–∞—á–∏–Ω–∞–µ—Ç—Å—è –æ—Ç —à=0 –∏ –æ–±—Ä—ã–≤–∞–µ—Ç—Å—è –Ω–∞ —Ç. –Ω, —á–∞—Å—Ç–æ—Ç–µ –î–µ–±–∞—è WD> –∫-—Ä–∞—è –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç—Å—è —É—Å–ª–æ–≤–∏–µ–º —Ä–∞–≤–µ–Ω—Å—Ç–≤–∞ –ø–æ–ª–Ω–æ–≥–æ —á–∏—Å–ª–∞ –∫–æ–ª–µ–±–∞–Ω–∏–π —á–∏—Å–ª—É —Å—Ç–µ–ø–µ–Ω–µ–π —Å–≤–æ–±–æ–¥—ã
PU)D "-- "-3
–æ
–û
–æ—Ç–∫—É–¥–∞
V,
(3)
–õ–∏—Ç.: –õ–∞–Ω–¥–∞—É –õ. –î., –õ –∏ —Ñ —à –∏ —Ü –ï. –ú., –°—Ç–∞—Ç–∏—Å—Ç–∏—á–µ—Å–∫–∞—è —Ñ–∏–∑—à—à, —á. 1, 3 –∏–∑–¥., –ú,, 1976; 3 –∞ –ò –º –∞ –Ω –î –∂., –ü—Ä–∏–Ω—Ü–∏–ø—ã —Ç–µ–æ—Ä–∏–∏ —Ç–≤–µ—Ä–¥–æ–≥–æ —Ç–µ–ª–∞, –ø–µ—Ä. —Å –∞–Ω–≥–ª., –ú,, 1974; –ê —à –∫ —Ä –æ —Ñ —Ç –ù., –ú –µ —Ä –º –∏ –Ω –ù., –§–∏–∑–∏–∫–∞ —Ç–≤–µ—Ä–¥–æ–≥–æ —Ç–æ–ª–∞, –ø–µ—Ä. —Å –∞–Ω–≥–ª., —Ç. 2, –ú., 1979. –í. –ú. –í–∏–Ω–æ-–∫—É—Ä, –≠. –ú. –≠–ø—à—Ç–ø–µ–π–Ω. –î–ï–ë–ê.–Ø –¢–ï–û–Ý–ò–Ø —Ç–≤‚ﶗĖ¥–æ–≥–æ —Ç–µ–ª–∞ ‚âà —Ç–µ–æ—Ä–∏—è, –æ–ø–∏—Å—ã–≤–∞—é—â–∞—è –∫–æ–ª–µ–±–∞–Ω–∏—è –∫—Ä–∏—Å—Ç–∞–ª–ª–∏—á, —Ä–µ—à‚ﶗǖ∫–∏ –∏ –æ–±—É—Å–ª–æ–≤–ª–µ–Ω–Ω—ã–µ –∏–º–∏ —Ç–µ—Ä–º–æ–¥–∫–Ω–∞–º–∏—á, —Å–≤–æ–π—Å—Ç–≤–∞ —Ç–≤‚ﶗĖ¥–æ–≥–æ —Ç–µ–ª–∞; –ø—Ä–µ–¥–ª–æ–∂–µ–Ω–∞ –ü- –î–µ–±–∞–µ–º –≤ 1912 –≤ —Å–≤—è–∑–∏ —Å –∑–∞–¥–∞—á–µ–π –æ —Ç–µ–ø–ª–æ‚ﶖº–∫–æ—Å—Ç–∏ –∫—Ä–∏—Å—Ç–∞–ª–ª–∞. –î- —Ç. –æ—Å–Ω–æ–≤–∞–Ω–∞ –Ω–∞ —É–ø—Ä–æ—â‚ï¶–Ω–Ω–æ–º –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω–∏–∏ —Ç–≤‚ﶗĖ¥–æ–≥–æ —Ç–µ–ª–∞ –∫–∞–∫ –∏–∑–æ—Ç—Ä–æ–ø–Ω–æ–π —É–ø—Ä—É–≥–æ–π —Å—Ä–µ–¥—ã, –∞—Ç–æ–º—ã –∫-—Ä–æ–π —Å–æ–≤–µ—Ä—à–∞—é—Ç –∫–æ–ª–µ–±–∞–Ω–∏—è –≤ –∫–æ–Ω–µ—á–Ω–æ–º –¥–∏–∞–ø–∞–∑–æ–Ω–µ —á–∞—Å—Ç–æ—Ç.
–ö—Ä–∏—Å—Ç–∞–ª–ª–∏—á. —Ä–µ—à‚ﶗǖ∫–∞, —Å–æ—Å—Ç–æ—è—â–∞—è –∏–∑ N —ç–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω—ã—Ö —è—á–µ–µ–∫ –ø–æ v –∞—Ç–æ–º–æ–≤ –≤ –∫–∞–∂–¥–æ–π, –∏–º–µ–µ—Ç 3^Vv‚âà–±« r^STVv –∫–æ–ª–µ–±–∞—Ç. —Å—Ç–µ–ø–µ–Ω–µ–π —Å–≤–æ–±–æ–¥—ã. –° –º–æ—Ö–∞–Ω–∏—á. —Ç–æ—á–∫–∏ –∑—Ä–µ–Ω–∏—è, —Ç–∞–∫—É—é —Å–∏—Å—Ç–µ–º—É –º–æ–∂–Ω–æ –æ–ø–∏—Å—ã–≤–∞—Ç—å –∫–∞–∫ —Å–æ–≤–æ–∫—É–ø–Ω–æ—Å—Ç—å –Ω–µ–∑–∞–≤–∏—Å–∏–º—ã—Ö –æ—Å—Ü–∏–ª–ª—è—Ç–æ—Ä–æ–≤, –∫–∞–∂–¥—ã–π –∏–∑ –∫-—Ä—ã—Ö —Å–æ-
–ü–ª–æ—Ç–Ω–æ—Å—Ç—å –∫–æ–ª–µ–±–∞—Ç. —Å–æ—Å—Ç–æ—è–Ω–∏–π –≤ –î. —Ç. –º–æ–∂–Ω–æ –∑–∞–ø–∏—Å–∞—Ç—å –≤ –≤–∏–¥–µ:
9 Afv ton/Co1* u) ^ —Å–æ, g(u)='
'D
Cl) > W
D
–í—Å–µ —Ç–µ—Ä–º–æ–¥–∏–Ω–∞–º–∏—á. —Ñ-—Ü–∏–∏ –≤ –î. —Ç. –º–æ–≥—É—Ç –±—ã—Ç—å –≤—ã—Ä–∞–∂–µ–Ω—ã —á–µ—Ä–µ–∑ —Ç. —è. —Ñ-—Ü–∏—é –î–µ–±–∞—è:
(5)
–°–≤–æ–±–æ–¥–Ω–∞—è —ç–Ω–µ—Ä–≥–∏—è F, —ç–Ω—Ç—Ä–æ–ø–∏—è S, –≤–Ω—É—Ç—Ä. —ç–Ω–µ—Ä–≥–∏—è £ –∏ —Ç–µ–ø–ª–æ‚ﶖº–∫–æ—Å—Ç—å –ø—Ä–∏ –ø–æ—Å—Ç, –æ–±—ä‚ﶖº–µ –°—É –æ–ø—Ä–µ–¥–µ–ª—è—é—Ç—Å—è —Ñ-–ª–∞–º–∏:
r{31n[l≈охр(-Оо/Г)] ≈flfflD/Г)}, (6)
(Go/?1) ≈ 3Afvfcln[l ≈ exp (≈Go/ЛЬ (V)
g^--Ne0 + 3NvkTD (6D/71), (8)
Су = 3/Vvfe [D (е0/Г) ≈(во/Л D' (в0/Г)], (9) 573
")
}