Однако градиентная инвариантность оставляет ещ╦ нек-рый произвол: к П? можно добавить (без изменения Е и Н] градиент любой ф-ции 1|э, удовлетворяющей ур-нию Пф≈ 0. Благодаря этому поля вне источников могут быть описаны лишь двумя компонентами Г. в. Часто в качестве таковых выбирают к.-л. декартову составляющую Пе и Пст, получая тем самым разделение поля ыа поперечно-магн. (ТМ) и поперечно-электрич. (ТЕ) моды. Внутри области, содержащей источники, в общем случае необходимо привлекать три компоненты Г. в.
Лит.; Сгрэттон Д, А., Теория электромагнетизма t [дер. с англ.], М.~ Л,, 1948; В а и н ш т е и н Л. А., Электромагнитные волны, М., 1957. М. Л. Миллер, Ю. А. Рыжов.
ГЕРЦА ВИБРАТОР ≈ металлич. антенна, имеющая форму штыря с утолщениями на концах и разрывом посредине для подключения источника (в режиме излучения) или нагрузки (в режиме при╦ма). Г. в. предложен Г. Р. Герцем в 1888, продемонстрировавшим с его помощью существование эл.-магн. волн, что послужило первым и наиб, веским доводом в пользу максвелловской теории электромагнетизма. Герц применял медные стержни с металлич* шарами или полосами на концах. _и искровым промежутком между ними, подключ╦нные к индукц. машине. Наименьший из применявшихся Герцем вибраторов имел длину / ≈ 26 см при частоте излучения v=5-108 Гц (длина волны Х^бО см). Г. в. явился родоначальником широкого семейства современных вибраторных антенн, многие из к-рых сохранили конструктивные особенности Г. в. Длина плеч вибраторов^ конструктивно подобных Г. в. (за исключением утолщений на концах штырей), обычно составляет /^ <0,5 К. При l<g,k характеристики вибратора совпадают с характеристиками элементарного электрич. диполя, в частности его сопротивление излучения пропорционально (ЦК)2. Это приводит к трудностям согласования с питающим трактом (фидером), генератором или нагрузкой, что в конечном сч╦те ы является причиной малой эффективности таких антенн, широко применяемых в ДВ-диапазонах, где приходится мириться с неравенством l<g,K во избежание сооружения слишком громоздких антенных устройств. В КВ-диапазонах эти ограничения отсутствуют, тогда оказываются предпочтительными резонансные (как правило, полуволновые, J"~Q,5 А.) вибраторы, сопротивление излучения к-рых близко к значению волновых сопротивлений стандартных фидеров.
Лит. см. при сг. Антенна. М. А. Миллер, В. И, Турчин. ГЕРЦА ПРИНЦИП (принцип наименьшей кривизны) ≈ один из вариационных принципов механики, согласно к-рому при отсутствии активных сил из всех кинематически возможных, т. е. допускаемых наложенными связями траекторий, действительной будет траектория, имеющая наим. кривизну, или «прямейшая». По этой причине Г. п., наз. принципом прямейшего пути, можно рассматривать как обобщение галилеева инерции закона. При применении Г. п. к механич. системе, состоящей из п материальных точек, под траекторией системы понимают кривую в Зп-мерном пространстве, элемент дуги к-рой определяется равенством
где М ≈ масса всей системы, т,- и dsf ≈ массы и элементы траекторий отд. точек. Г. п. тесно связан с принципом иаим. принуждения Гаусса (см. Гаусса принцип) и при идеальных связях имеет такое же матем. выражение (6Z=0, где Z ≈ принуждение), т. к, кривизна Зя-мерной траектории системы пропорциональна корню квадратному из принуждения, Г. п. примен╦н Г. Р. Герцем для построения его механики, в к-рой действие активных сил заменяется введением соответствующих связей. С. М, Taps. Г╗РЦШПРУНГА ≈ Р╗ССЕЛЛА ДИАГРАММА ≈ гра-фич. изображение зависимости абс. зв╦здная величина ≈ спектральный класс зв╦зд. Вместо спектрального класса
в качестве координаты на графике могут использоваться показатель цвета или эффективная температура звезды, а вместо абс. зв╦здной величины ≈ светимость звезды. Спектральный класс к показатель цвета определяются в основном темп-рой звезды. Следовательно, положение звезды на Г.≈Р. д. характеризует соотношение между е╦ важнейшими наблюдаемыми параметрами ≈ темп-рой и
Спектральный класс О BO,IB2B5B8B9 AOA2A3A5 FOF2F5 F8GO G5 KQK2K5 М
-Б
-5
-А
-3
-2
OJ
ш
+2 +3 +4
S +5
m
+6
+7
+9 + 10 + 11 +12 +13 +14 +15
Т≈|≈|≈J≈I≈I≈I≈\≈I≈Г
≈i≈i≈i≈i≈i≈i≈г~т Полоса нестабильности
I
Белые карлики .* ∙ ' *
i т
Ш
U
и
ш
о.
<
X
с 3
о,
ш
2DOQQ 10000 8000 7000 6000 5000 Эффективная температура Гэ,К
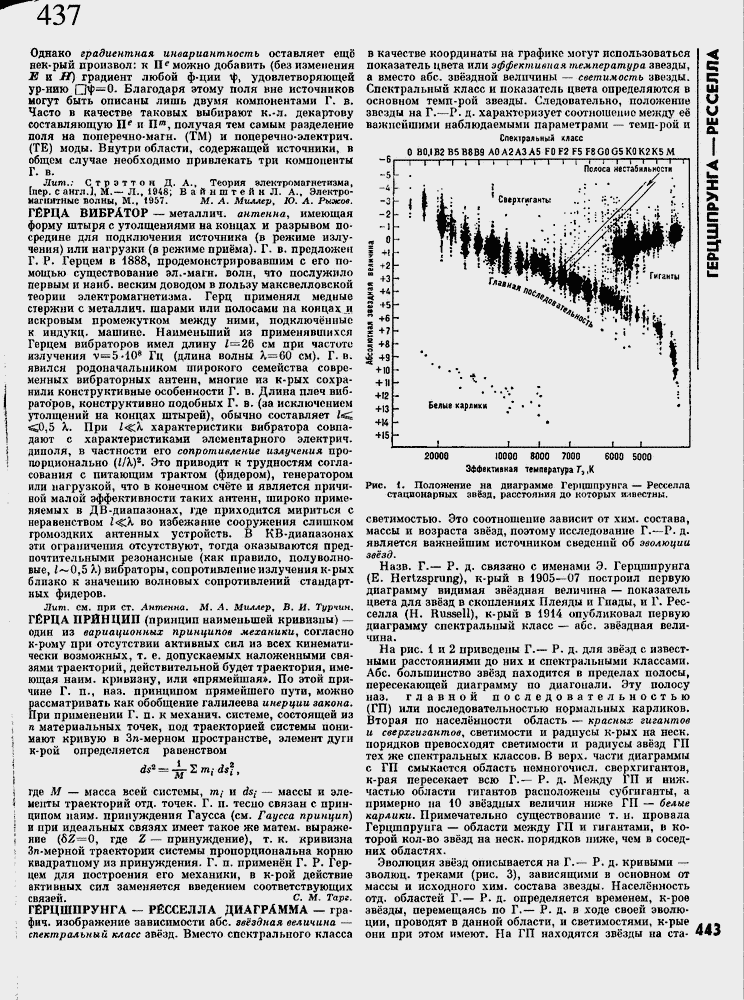
Рис, I, Положение на диаграмме Герцшпрунга ≈ Ресселла стационарных зв╦зд, расстояния до которых иавестны.
светимостью. Это соотношение зависит от хим. состава, массы и возраста зв╦зд, поэтому исследование Г.≈Р. д. является важнейшим источником сведений об эволюции зв╦зд.
Назв. Г.≈ Р. д. связа-но с именами Э. Герцшпрунга (Е. Hertzsprung), к-рый в 1905≈07 построил первую диаграмму видимая зв╦здная величина ≈ показатель цвета для зв╦зд в скоплениях Плеяды и Гиады, и Г, Ресселла (Н. Russell), к-рый в 1914 опубликовал первую диаграмму спектральный класс ≈ абс. зв╦здная величина.
На рис. 1 и 2 приведены Г.≈ Р. д. для зв╦зд с известными расстояниями до них и спектральными классами. Абс. большинство зв╦зд находится в пределах полосы, пересекающей диаграмму по диагонали. Эту полосу паз. главной последовательностью (ГП) или последовательностью нормальных карликов. Вторая по насел╦нности область ≈ красных гигантов и сверхгигантов, светимости и радиусы к-рых на неск. порядков превосходят светимости и радиусы зв╦зд ГП тех же спектральных классов. В верх, части диаграммы с ГП смыкается область пемногочисл. сверхгигантов, к-рая пересекает всю Г.≈ Р. д. Между ГП и ниж. частью области гигантов расположены субгиганты, а примерно па 10 зв╦здных величин ниже ГП ≈ белые карлики. Примечательно существование т. н. провала Герцшпрунга ≈ области между ГП и гигантами, в которой кол-во зв╦зд на неск. порядков ниже, чем в соседних областях.
Эволюция зв╦зд описывается на Г.≈ Р. д. кривыми ≈ зволюц. треками (рис. 3), зависящими в основном от массы и исходного хим. состава звезды. Населенность отд. областей Г.≈ Р. д. определяется временем, к-рое зв╦зды, перемещаясь по Г.≈ Р. д. в ходе своей эволюции, проводят в данной области, и светимостями, к-рые *** они при этом имеют. На ГП находятся зв╦зды на ста- 443
")
}


