ГЕЛЛ-МАНА≈ НИШИДЖПМЫ ФОРМУЛА ≈ ны-
ражает значение (в единицах е] электрцч. заряда Q адрона, принадлежащего данному изотопическому муль-типлету, через значение характеризующей его третьей проекции изотопического спина /3 и гиперзаряд Y: Q≈/зН-'/з У. Предложена М. Гелл-Мапом и независимо К. Нишиджимоп. (К, NishijiiYia) в 1953 для описания элсктрич. зарядов странных частиц. При этом предполагалось, что Y=B + S, где В ≈ барионное число, К ≈ странность. В дальнейшем выяснилось, что ф-ла имеет более общее значение и может быть применена для описания электрич. нарядов любых адроиов ≈ очарованных и др. (см. Гиперзаряд').
Г.-М.≈ 1Ь ф. иногда применяется и для описания элсктрич. зарядов лешпонов и кварков, группируемых в т. и. слабые и з о м у л ь т и п л е т ы. В этих случаях в нее подставляются значения третьей проекции слабого и з о с п и н а и слабого гиперзаряда соответственно для лептонов п кварков.
А. А. Комар.
ГЕЛЬМГОЛЬЦА УРАВНЕНИЕ ≈ дифференциальное уравнение ДгН-Яи≈0, где Д ≈ Лапласа оператор, К ≈ постоянная; при Я=0 Г. у. переходит в Лапласа уравнение. Г. у. можно получить из волнового уравнения, если зависимость от времени описывается функцией ехр(гшг), в этом случае Я≈ оА;~2 (с ≈ скорость распространения волн). Названо по имени Г. Гельмгольца (Н. HelmholtzJ, изучавшего это уравнение в I860.
Для Г- у. в ограниченной области рассматривают обычные краевые задачи (Дирихле, Неймана и др,}. Значения Я, для к-рых существует отличное от нуля решение однородного Г. у., наз. собственными значениями оператора Лапласа. Для таких значений Я, решение краевой задачи но единственно. При помощи ф-ции Гри-ца краевую задачу можно свести к интегральному ур-иию. В случае неограниченной области убывающее на бесконечности решение Г. у. не является единственным при Я>0. В этом случае для выделения единств, решения ставят дополнит, условия (см. Зоммерфельда условия излучения).
Лит.: Тихонов А. Н,, Самарский А. А., Уравнения математической физики. 5 изд., М., 1977; В л а д и м и-ров В. С., Уравнения математической физики, 4 изд., М., J.981, В. И. Алхимаа.
ГЕЛЬМГОЛЬЦА ЭНЕРГИЯ (свободная энергия, изо-хорно-изотермичсский потенциал) ≈ один из термодинамических потенциалов, характеристическая функция при выборе объ╦ма Уитсмп-ры Т в качестве независимых тсрмодинамич. переменных. Введена Дж. У. Гиб^ беом (J. W- Gibbs) в 1875, е╦ использовал Г. Гельмгольц в 1882, к-рому принадлежит термин «свободная энергия», В статистич. физике более распростран╦н термин «свободная энергия».
Существование Г. Э- есть следствие первого и второго начал термодинамики. Она связана с внутренней энергией V и энтропией S соотношением F=U≈TS (для Г. э. используют также обозначения А или 1У). Изменение Г. э. при квазистатнч. процессе равно dF= ≈ SdT≈PdV, следовательно, убыль Г. а. при изо-тсрмич. процессе равна полной работе, совершаемой системой. Энтропию и давление можно получить, дифференцируя Г. э. по Т и V: S = ≈ (dF!OT)v, Р^~- (dF/dV)T. Это означает, что Г. э. есть характеристич. ф-ция в переменных Т и У. Для многокомпонентных систем
dF^ ≈ SdT≈PdV+^.wdN[, где dNf ≈ приращение
массы i-ro компонента, u/= (OFldNfir, v ≈ хим. потенциал. Условием термодшзамич. равновесия системы является минимум Г. э. при постоянстве Т, V и др. термодннамич. параметров, определяющих состояние системы.
В статнстич. физике Г. о. определяется через логарифм статистич. интеграла (или статистич. суммы) Z; f=≈kT In Z.
Лит. см. при ст. Термодинамики. Д. Н. Зубарев.
ГЕНЕРАТОР ГРУППЫ (от лат. generator ≈ производи-тель) (инфинитезимальный оператор) ≈ точнее, генератор представления Tg-^T(q>1, ..., fp") группы Ли G, параметризованной в окрестности е╦ единичного элемента е канонич. параметрами <ра,≈ оператор l&=dTjdy I a_0.
Канонич. параметризация всегда существует и означает, что g (0, . ..,()) =0, а элементы G вида g (0, ... ,фа, .. .0) окрестность однопараметрнч. подгруппы Г.г. 1а порождают Ли алгебру представи удовлетиоряют соотношениям [/а, 1$ ] ≈
≈ структурные константы алгебры.
образуют группы О
ления
g
Если представление Tg унитарно, Г. г. /« аытипрми-тоньт; в финике принято вводить эрмитов базис в алгебре Ли: La ≈ if а- В квантовой теории физ. величинам соответствуют эрмитовы операторы L«. Напр., для группы вращений 0{3) параметры фа соответствуют. углам поворотов вокруг осей х, (/, 2, Г. г. ≈ колшонентам угл* момента Л1а, а соотношения алгебры Ли ≈ перестановочным соотношениям для Ма- [^«) jWpl^^aPv^v В класеич. механике, где алгебру Ли порождают Пуассона скобки, Г. г. реализуются как ф-ции канонич. церемонных. Важным примером является группа калибро-мчных преобразований, для к-рой Г. г. ≈ связи первого рода (СМ, Гамилътонов формализм).
Лит.; Б о г о л ю б о в II, Н., Л о г у нов А. А., Т о-д о р о в И. Т., Основы аксиоматического подхода D кпантовой теории поля, М., Ш9, гл. 2, доп. А; Румер Ю, Б,, Ф с т А. И., Теории унитарной симметрии, М., 11)70; Э л л и-от Дж,, Добер П., Симметрия в физике, пер. с англ., т. 1 ≈ 2, М., 198Я. В. П. Яоллов.
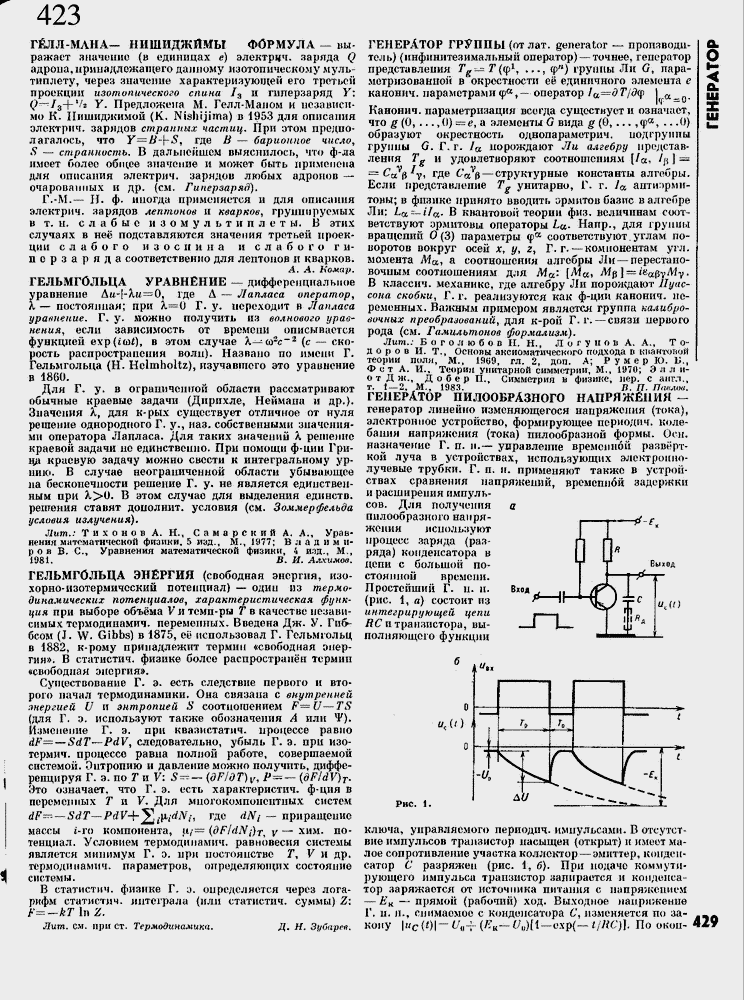
ГЕНЕРАТОР ПИЛООБРАЗНОГО НАПРЯЖЕНИЯ ≈
генератор линейно изменяющегося напряжения (тока),
электронное устройство, формирующее периодич. коле-
бания напряжения (тока) пилообразной формы. Осн.
назначение Г. п. п. ≈ управление временной разверт-
кой луча в устройствах, использующих электронно-
лучевые трубки. Г. п. п. применяют также в устрой-
ствах сравнения напряжений, временной задержки
и расширения импуль-
сов. Для получения с
пилообразного напря-
жения используют
процесс заряда (раз-
ряда) коЕ1денсатора в
цепи с большой по-
стоянной времени.
Простейший Г. и- п.
(рис. 1, я) состоит из
интегрирующей цепи
ЛС и транзистора, вы-
полняющего функции
Вход
Рис. 1.
ключа, управляемого периодич. импульсами. В отсутствие импульсов транзистор насыщен (открыт) н имеет малое сопротивление участка коллектор ≈ эмиттер, конденсатор С разряжен (рис. 1, 6). При подаче коммутирующего импульса транзистор запирается и конденсатор заряжается от источника питания с напряженней ≈ Ек ≈ прямой (рабочий) ход. Выходное напряжение Г. п. л., снимаемое с конденсатора С, изменяется по закону \itc(t)\\≈Ut^--(Яи≈ /Л)[1≈ехр{≈ tjRC)]. По окоо
а О
а ш
X ш
429
")
}


