на рассмотренных моделях, не позволяют достаточно строго интерпретировать эксперим. данные, т, к. пока не уда╦тся учитывать энергетич. неоднородность поверхности, связанную с разл. природой центров А. Осн. термодинамич. ур-нием, описывающим А., является ур-ние Гиббса:
где а ≈ поверхностное натяжение на границе раздела, j.i ≈ химический потенциал адсорбата. Ур-ние Гиббса можно использовать в качестве исходного для вывода ур-ний А. при разл. условиях. К ним, в первую очередь, относятся ур-ния изотерм А., представляющие собой зависимость кол-ва адсорбир. вещества от давления р (или концентрации) адсорбата при пост, темп-ре.
Теория Ленгмюра позволяет вывести ур-ние одной из наиб, простых изотерм А., справедливое при строгой энергетич. однородности поверхности адсорбента, а также при отсутствии на поверхности латерального взаимодействия:
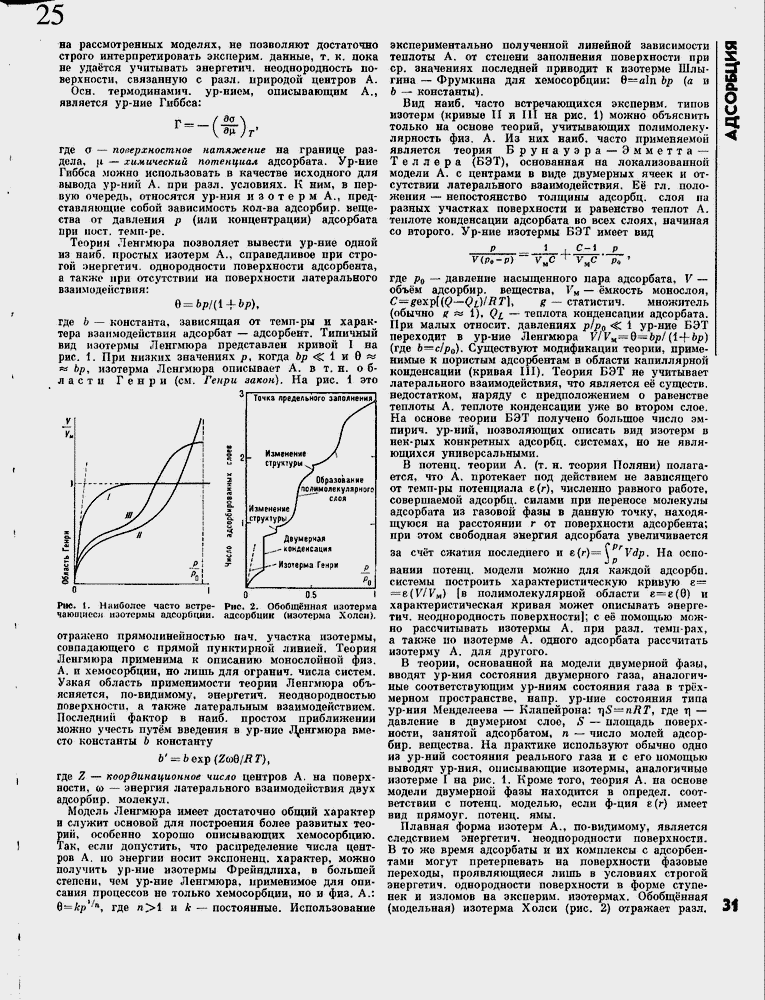
где Ь ≈ константа, зависящая от темп-ры и характера взаимодействия адсорбат ≈ адсорбент. Типичный вид изотермы Ленгмюра представлен кривой I на рас. I. При низких значениях р, когда Ър < 1 и 9 » « Ьр, изотерма Ленгмюра описывает А. в т.н. области Генри (см. Генри закон). На рис. 1 это

са <и
о
Л
ш о
га
о
I
Тачка предельного заполнения
Изменение струшуры
j
Образование полимолекулярного
слоя
Изменение _структурь
Двумерная ,- конденсация
Изотерма Генрк
О 05 I
Рис. I, Наиболее часто ветре- Рис. 2, Обобщ╦нная изотерма чающиеся изотермы адсорбции, адсорбции (изотерма Холси},
отражено прямолинейностью нач. участка изотермы, совпадающего с прямой пунктирной линией. Теория Ленгмюра применима к описанию монослойной физ. А, и хемосорбции, но лишь для огранич. числа систем. Узкая область применимости теории Ленгмюра объясняется, по-видимому, энергетич:. неоднородностью поверхности, а также латеральным взаимодействием. Последний фактор в наиб, простом приближении можно учесть пут╦м введения в ур-нио Ленгмюра вместо константы Ъ константу
где Z ≈ координационное число центров А. на поверхности, со ≈ энергия латерального взаимодействия двух адсорбир, молекул.
Модель Ленгмюра имеет достаточно общий характер и служит основой для построения более развитых теорий, особенно хорошо описывающих хемосорбцию. Так, если допустить, что распределение числа центров А, по энергии носит экспоненц. характер, можно получить ур-ние изотермы Фрейндлиха, в большей степени, чем ур-ние Ленгмюра, применимое для описания процессов не только хемосорбции, но и физ. А.:
6 ≈ kp n, где п>1 и А- ≈ постоянные. Использование
экспериментально полученной линейной зависимости теплоты А. от степени заполнения поверхности при ср. значениях последней приводит к изотерме Шлы-гина ≈ Фрумкина для хемосорбции: 0≈aln Ър (а и b ≈ константы).
Вид наиб, часто встречающихся эксперим. типов изотерм (кривые II и III на рис. 1) можно объяснить только на основе теорий, учитывающих полимолеку-лярность физ. А. Из иих наиб, часто применяемой является теория Брунауэра ≈ Эмметта ≈ Т е л л е р а (БЭТ), основанная на локализованной модели А. с центрами в виде двумерных ячеек и отсутствии латерального взаимодействия. Е╦ гл. положения ≈ непостоянство толщины адсорбц. слоя па разных участках поверхности и равенство теплот А. теплоте конденсации адсорбата во всех слоях, начиная со второго. Ур-ние изотермы БЭТ имеет вид
Р 1 , С-\\ о
где PQ ≈ давление насыщенного пара адсорбата, V ≈ объ╦м адсорбир. вещества, VH ≈ ╦мкость монослоя, <?=#ехр[(ф≈QtfjftT], g ≈ статистич. множитель (обычно ц т 1), QL ≈ теплота конденсации адсорбата. При малых относит, давлениях р/р$ <: 1 ур-ние БЭТ переходит в ур-ние Ленгмюра 7/FM~0=&p/(l-f&p) (где Ь=с/р0). Существуют модификации теории, применимые к пористым адсорбентам в области капиллярной конденсации (кривая III). Теория БЭТ не учитывает латерального взаимодействия, что является е╦ существ, недостатком, наряду с предположением о равенстве теплоты А. теплоте конденсации уже во втором слое, На основе теории БЭТ получено большое число эм-пирич. ур-ний, позволяющих описать вид изотерм в нек-рых конкретных адсорбц. системах, но не являющихся универсальными.
В потенц, теории А. (т. н. теория Поляки) полагается, что А. протекает под действием не зависящего от темгг-ры потенциала е(г), численно равного работе, совершаемой адсорбц. силами при переносе молекулы адсорбата из газовой фазы в данную точку, находящуюся на расстоянии г от поверхности адсорбента; при атом свободная энергия адсорбата увеличивается
за сч╦т сжатия последнего и e(r)=\\ Vdp. На основании потенц, модели можно для каждой адсорби. системы построить характеристическую кривую е≈ = е (W7М) [в полимолекулярной области е= е (9) и характеристическая кривая может описывать эперге-тич. неоднородность поверхности]; с е╦ помощью можно рассчитывать изотермы А. при разл. теми-рах, а также по изотерме А. одного адсорбата рассчитать изотерму А. для другого.
В теории, основанной на модели двумерной фазы, вводят ур-ния состояния двумерного газа, аналогичные соответствующим ур-ниям состояния газа в трехмерном пространстве» напр, ур-ние состояния типа ур-ния Менделеева ≈ Клапейрона: i\\S≈пЯТ, где t] ≈ давление в двумерном слое, S ≈ площадь поверхности, занятой адсорбатом, п ≈ число молей адсорбир. вещества. На практике используют обычно одно из ур-ний состояния реального газа и с его помощью выводят ур-ния, описывающие изотермы, аналогичные изотерме I на рис. 1. Кроме того, теория А, на основе модели двумерной фазы находится в определ. соответствии с потенц. моделью, если ф-ция г (г) имеет вид прямоуг. потенц. ямы.
Плавная форма изотерм А., по-видимому, является следствием энергетич. неоднородности поверхности. В то же время адсорбаты и их комплексы с адсорбентами могут претерпевать на поверхности фазовые переходы, проявляющиеся лишь в условиях строгой энергетич. однородности поверхности в форме ступенек и изломов на эксперим, изотермах. Обобщ╦нная (модельная) изотерма Холси (рис. 2) отражает разл.
О U
31
")
}



