атомы предполагается неразличимыми и в каждой ячейке может находиться произвольное; число частиц. Поэтому статистич, вес W(Nf} равен числу различных
распределений частиц по ячейкам:
он определяет вероятность распределения частиц по ячейкам. Энтропия такого состояния равна S~k In W. Наиболее вероятному состоянию отмечает максимум энтрошш (при заданных £ =
и
__
распределение Бозе ≈ Эйнштейна л,≈ =Ar//<V Энтропия идеального газа, подчиняющегося Б.≈ Э.с,, равна
= 2 G<*
«,-)
Одним из применений Б.≈ Э, с, является теория тепло╦мкости тв╦рдых тел. Тепловые колебания тв╦рдого тела описываются как возбуждения сопокушюсти осцилляторов, соответствующих нормальным колебаниям крнсталлич. реш╦тки. Возбужд╦нные состояния
∙системы осцилляторов можно описывать как идеальный газ квазичастиц ≈ фонопов, подчиняющихся Б.≈ Э. с. На основании этого представления уда╦тся правильно
∙описать поведение твердых тел при низких темл-рахт в частности получить Дебая закон тепло╦мкости. К важным приложениям Б. ≈ Э. с. относится также теория излучения ч╦рного тела, опирающаяся на представление о квантах эл.-магн. поля ≈ фотонах. Последние подчиняются Б.≈ Э. с.: в атом случае ц=0, а £/ ≈ ^=hv (v ≈ частота излучения). При этом распределение Бозе ≈ Эйнштейна да╦т Планка закон излучения для
∙спектрального распределения энергии излучения абс. ч╦рного тела.
Б.≈ Э. с. для системы взаимодействующих частиц основана на методе Гиббса для квантовых систем. Она может быть реализована, если известны квантовые уровни системы ╦п и подда╦тся вычислению статистическая
∙сумма
тде суммирование вед╦тся но всем квантовым уровням системы для состояний, удовлетворяющих условиям квантовой симметрии. Последнее условие определяет тин квантовой статистики. Задача вычисления Z не ∙сводится к простой комбинаторной задаче и очень сложна, если взаимодействие между частицами не мало. Е╦ можно несколько упростить, если выразить гамильтониан системы н представлении вторичного квантования (в представлении чисел заполнения квантовых уровней) через операторы вторичного квантования т (x), Y + fc), удовлетворяющие перестановочным соотношениям Б.≈ - Э. с.
где б (я≈ г') -- дельта-функция Дирака. Тогда требования Б.≈ Э. с. оказываются выполненными и в статистич, сумме будут учитываться лишь симметричные состояния. Но и в такой постановке задача вычисления статистич. суммы очень сложна и допускает приближ╦нное решение лишь для слабовзаимодействующих систем (елабонеидсальный бозе-газ).
Лит.: Л а н д а у Л. Д., Л и ф ш и ц Е. М., Статистическая физика, ч. 1, у изд., м., 1970; М а и е р Д ж., Г е гт л е р т-Майер М., Статистическая механика, пер. с англ., 2 изд., Мм 19ЬО, гл. 7; X у а н г К., Статистически л механика, пер] «англ., М., 1966; Боголюбов Н. Н., Лекции па кванто-слг*СЛы"тСтГШ1£ Иябр' ТРТОЫ, т. 2, К., 1070. Д, Н. ЗуСмрев. ЫМОНЫ (бозе-частицы) ≈ частицы или кваэичасти-цы с нулевым ЕЛИ целочисленным спином; подчиняются Базе ≈ Эйнштейна статистике. К ним относятся фотон, промежуточные векторные бозоны, глюопы {спин 1). гравит-он (спин 2), гипотетические голдстоу-бозоны и Хигзса бозоны (спин 0), а также сос-
тавные частицы из ч╦тного числа фермионов, напр. вес мезоны, «построонные» из кварка и антикнарка, атомные ядра с ч╦тным числом нуклонов (дейтрон, ядро 4Не и т. п.). Ti. являются также фонопы в твердом теле и в жидком 4Не, экситоны в полупроводниках и ди-элект р иках и др.
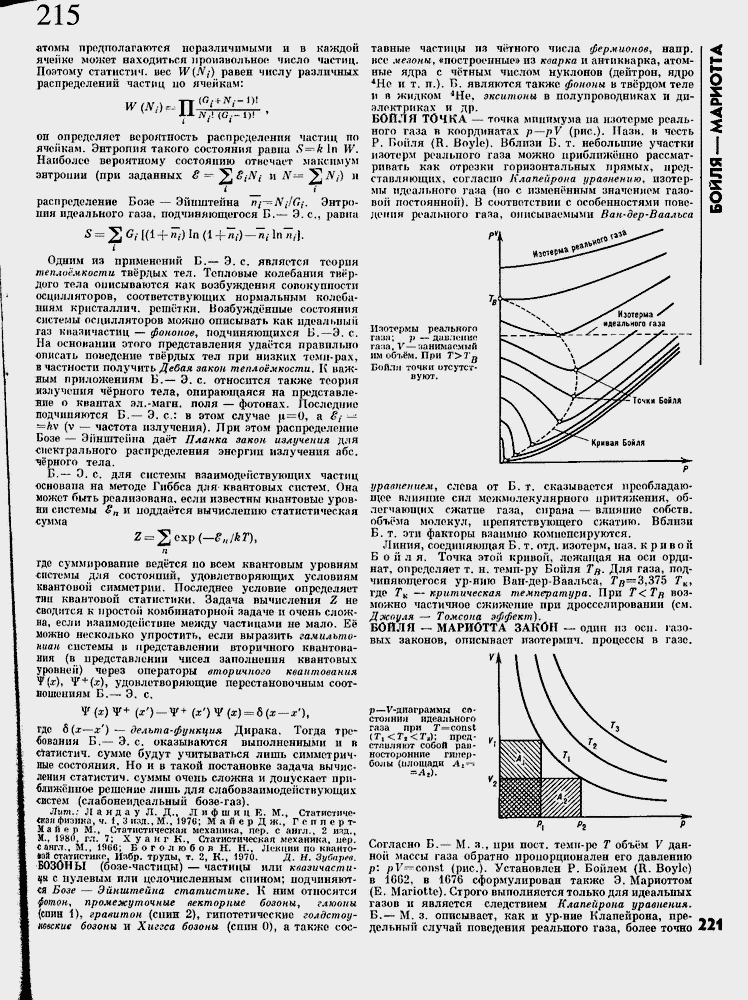
БОЙ Л Я ТОЧКА ≈ точка минимума иа изотерме реального газа в координатах р≈ pV (рис.). ГТазн. в честь Р. Бойля (R. Boyle). Вблизи Б. т. небольшие участки изотерм реального газа можно приближ╦нно рассматривать как отрезки горизонтальных прямых, представляющих, согласно Клапейрона уравнению, изотермы идеального газа (но с измен╦нным значением газовой постоянной). В соответствии с особенностями поведения реального газа, описываемыми Ван-дер-Ваалъса
Изотермы реального та ад; р ≈даилспж» ra:ta, V≈Ечанимаолплй им объ╦м. При Г>2'п
Бойля точки отсутствуют.
Изотерма идеального газа
уравнением, слева от Б. т. сказывается преобладающее влияние сил межмолекулярного притяжения, об-легмающих сжатие газа, справа ≈ влияние собств. объ╦ма молокул, препятствующего сжатию. Вблизи Б. т. эти факторы взаимно компенсируются.
Линия, соединяющая Б. т. отд. изотерм, паз. кривой Б о и л я. Точка этой кривой, лежащая на оси ординат, определяет т. н. темп-ру Бойля Т%. Для газа, подчиняющегося ур-ниго Ваи-дер-Ваалъса, Гд≈3,375 ГК1 где Tk ≈критическая температура. При T<TR возможно частичное сжижение при дросселировании (см. Джоуля ≈ Томсола эффект],
БОЙЛЯ ≈ МАРИОТТА ЗАК01Г ≈ один из осп. газовых законов, описывает изотермпч. процессы в газе.
р≈V-диаграммы состоянии идеального газа при Т=const
IT1 _-* f1 ^- Т* \\ - -_-_ ≥1 <тз<Тя), ПрСД- v
стпиляют собой рал- ' посторонние гинер-Оолы (площади А,^--
I
Согласно Б.≈ М. з., при пост, темн-ре Т объем V данной массы газа обратно пропорционален его давлению р: рT^const <рис,). Установлен Р. Бойлеи (R. Boyle) в 16G2, в 1676 сформулирован также Э. Мариоттом (Е. Mariotte). Строго выполняется только для идеальных газов и является следствием Клапейрона уравнения. Б.≈ М, з, описывает, как и ур-ние Клапейрона, предельный случай поведения реального газа, более точно 221
")
}


