(–≤ —В. —З. —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є, –Љ–µ—Е–∞–љ–Є–Ї–Є, –≥–Є–і—А–Њ–і–Є–љ–∞–Љ–Є–Ї–Є) –њ—А–Є–Љ–µ–љ–Є—В–µ–ї—М–љ–Њ –Ї —В–µ–Љ –і–µ—В–∞–ї—П–Љ –Љ–Њ–і–µ–ї–Є, –≥–і–µ –њ–Њ—Б–ї–µ–і–љ–Є–µ –Њ–њ—А–∞–≤–і–∞–љ—Л. –≠—В–Њ—В –њ–Њ–і—Е–Њ–і —Е–∞—А–∞–Ї—В–µ—А–µ–љ –і–ї—П –С. –љ–∞ –≤—Б–µ—Е –µвХ¶ —Г—А–Њ–≤–љ—П—Е: –Њ—В –Љ–Њ–ї–µ–Ї—Г–ї—П—А–љ–Њ–≥–Њ –і–Њ –±–Є–Њ—Б—Д–µ—А—Л –≤ —Ж–µ–ї–Њ–Љ.
–Ы–Є—В.: –С –ї —О –Љ —Б –Є —Д (' –ї —М –і –Ы. –Р., –Я—А–Њ–±–ї–µ–Љ—Л –±–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Њ–є —Д–Є^–Є–њ–Є, 2 –Є–ї–і., –Ь,, 1–£77; –Т –Њ –ї —М –Ї –† –љ —И —В —Б –Є –љ –Ь. –Т., –Ь–Њ–ї–µ–Ї—Г–ї—П—А–љ—П–љ –±–Є–Њ—Д–Є–Ј–Є–Ї–∞, –Ь.. 197ii; –µ–≥–Њ –ґ –Њ, –Ю–±—Й–∞)! –±–Є–Њ—Д–Є–Ј–Є–Ї–∞, –Ь., HITS; —П –≥ fi –ґ –Є, –С–Є–Њ—Д–Є–Ј–Є–Ї–∞, –Ь., 1S181; –† –Њ –Љ —П –Ї –Њ –Є-–≥, –Ї –Є –Є –Ѓ. –Ь. , –°—В–µ–њ–∞–љ –Њ –≤ –∞ –Ш. It. , –І « —А –љ –∞ –≤-—Б–Ї–Є–є –Ф. –°., –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Љ–Њ–і–µ–ї—Й–Ї—И–∞—И–≥–≥ –Є –С–Є–Њ—Д–Є–Є–Є–Ї–Њ, –Ь., 1975; –Є—Е –ґ –†, –Ь–∞—В–µ–Љ–∞—В–Є—З–≥—Б–Ї–∞–њ –±–Є–Њ—Д–Є–Ј–Є–Ї–∞, –Ь., 111–Э4; –Ш –љ –∞-–љ –Є —Ж –Ї –Є ti –У. –†., –Ъ —А –Є –Є –Њ –Ї –Є fi –Т. –Ш., –° –≥ –ї –≥, –Ї –Њ –≤ –Х. –Х., –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—П –±–Є–Є—Д–Є–ї–Є–Ї–∞ –Ї–ї–µ—В–Ї–Є, –Ь., 11)78.
–Ф. –°, –І–µ—А–њ–∞–µ—Б–Ї—Й.
–С–Ш–Я–Ю–Ы–ѓ–†–Ю–Э (–Њ—В –ї–∞—В. –Ђ-, –≤ —Б–ї–Њ–ґ–љ—Л—Е —Б–ї–Њ–≤–∞—Е вЙИ –і–≤–Њ–є–љ–Њ–є. –і–≤–Њ—П–Ї–Є–є –Є –≥—А–µ—З, polos вЙИ –Њ—Б—М, –њ–Њ–ї—О—Б) вЙИ —Б–Є—Б—В–µ–Љ–∞, —Б–Њ—Б—В–Њ—П—Й–∞—П –њ–∞ –і–≤—Г—Е —Н–ї–µ–Ї—В—А–Њ–љ–Њ–≤ –њ—А–Њ–≤–Њ–і–Є–Љ–Њ—Б—В–Є, —Б–љ—П—П–∞–љ-–≤—Л—Е –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є –±–ї–∞–≥–Њ–і–∞—А—П —Б–Є–ї—М–љ–Њ–Љ—Г –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є—О —Б–Њ —Б—А–µ–і–Њ–є. –Я. –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є 2 —Б–≤—П–Ј–∞–љ–љ—Л—Е –њ–Њ–ї—П—А–Њ–љ–∞. –Ґ–∞–Ї–Є–µ —Б–≤—П–Ј—Л–≤–∞–љ–Є–µ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –≤ –ґ–Є–і–Ї–Њ—Б—В—П—Е, –Ї—А–Є—Б—В–∞–ї–ї–∞—Е, –∞–Љ–Њ—А—Д–љ—Л—Е –≤–µ—Й–µ—Б—В–≤–∞—Е. –Х—Б–ї–Є –≤–Њ –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є–Є —Б–Њ —Б—А–µ–і–Њ–њ –і–Њ–Љ–Є–љ–Є—А—Г–µ—В –Є–ї—Б–Ї—В—А–Є—З. –њ–Њ–ї—П—А–Є–Ј–∞—Ж–Є—П, —В–Њ —Г—Б–ї–Њ–≤–Є–µ–Љ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –Ы . —П–≤–ї—П–µ—В—Б—П 6ojj —Л–Љ–∞—П –і–Є–∞–ї–µ–Ї—В —А–Є—З. –њ—А–Њ–љ–Є—Ж–∞–µ–Љ–Њ—Б—В—М —Б—А–µ–і—Л. –Ґ–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П –С. –±—Л–ї–∞ –Њ–±–Њ—Б–љ–Њ–≤–∞–љ–∞ –љ–∞ –њ—А–Є–Љ–µ—А–µ –Є–Њ–љ–љ—Л—Е –Ї—А–Є—Б—В–∞–ї–ї–Њ–≤ [1] –Є —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–∞ –љ–∞ —Б–ї—Г—З–∞–є –∞–Љ–Њ—А—Д–љ—Л—Е –њ–Њ–ї—Г–њ—А–Њ–≤–Њ–і–љ–Є–Ї–Њ–≤ |2], –Љ–µ—В–∞–ї–ї–Њ–≤ –Є –і—А. –Т –С, —Б–≤—П–Ј—Л–≤–∞—О—В—Б—П —Н–ї–µ–Ї—В—А–Њ–љ—Л —Б –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л–Љ–Є —Б–њ–Є–љ–∞–Љ–Є; —Б–≤–Є–і–µ—В–µ–ї—М—Б—В–≤–Њ –Є—Е —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П вЙИ –Њ—В—Б—Г—В—Б—В–≤–Є–µ –њ–∞—А–∞–Љ–∞–≥–љ–µ—В–Є–Ј–Љ–∞ —Б–≤–Њ–±–Њ–і–љ—Л—Е –љ–Њ—Б–Є—В–µ–ї–µ–є –Ј–∞—А—П–і–∞. –≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–µ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–∞ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П –С. –њ–Њ–ї—Г—З–µ–љ—Л –і–ї—П —А—П–і–∞ –Ї—А–Є—Б—В–∞–ї–ї–Њ–≤ –Њ–Ї–Є—Б–ї–Њ–≤ —Б –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є –≤–∞–ї–µ–љ—В–љ–Њ—Б—В—М—О (–љ–∞–њ—А., Ti407 [3]), –≤ –љ–µ–Ї-—А—Л—Е —Б–Њ–µ–і–Є–љ–µ–љ–Є—П—Е –ї–Є–љ–µ–є–љ—Л—Е –Њ—А–≥–∞–љ–Є—З. –Љ–Њ–ї–µ–Ї—Г–ї [4]. –Я—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ–Њ-–≤—А–µ–Љ–µ–љ–љ—Л–µ –Є —Н–љ–µ—А–≥–µ—В–Є—З. –Љ–∞—Б—И—В–∞–±].! –ђ. –Є–љ—Л–µ, —З–µ–Љ –≤ –Ї—Г–њ–µ—А–Њ–Є—Б–Ї–Њ–є –њ–∞—А–µ. –Я–Њ–Ј–µ вЙИ –≠–є–љ—И—В–µ–є–љ–∞ –Ї–Њ–љ–і–µ–љ—Б–∞—Ж–Є—П –С. –Љ–Њ–ґ–µ—В –њ—А–Є–≤–µ—Б—В–Є –Ї –±—И–ґ—Б–Є—В–Њ—И—О–њ —Б–≤–µ—А—Е–њ—А–Њ–≤–Њ–і–Є–Љ–Њ—Б—В–Є, –Њ–±–ї–∞–і–∞—О—Й–µ–є —Е–∞—А–∞–Ї—В–µ—А–љ—Л–Љ–Є –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В—П–Љ–Є, –Ы–Є—В.: 1) –Т –Є –љ (–Ь[ –Ї –Є ii –Т. ,–Я., –Ю –±–Є–њ–Њ–ї—П—А–љ—Л—Е –Є–Њ—Б—В–Њ—Ж–Є–Є–ї—Е –љ–Њ—Б–Є—В–µ–ї–µ–є —В–Њ–Ї–∞ –≤ –Є–Њ–љ–љ—Л—Е –Ї—А–Є—Б—В–∞–ї–ї–∞—Е, «–Ц–≠–Ґ–§», 19(–Э, —В. 40, —Б. 145–Я; 2) A n d e r s —А –ї P. W.t Model for the electronic structure of amorphous semiconductors, «Phys. Rev. Lett.», 1975, v. 34, p. –£5;*; J) L a k k i s S. –Є –і—А., McLall-insulator transitions in Ti4Oj single1 crystals: Crystal characterisation, specific ln;at and EI'R, «Phys. Rev.», 11>76, v. –Ъ 1/—З —А. –Ш2–ѓ; 4) Srntt J. C. –Є –і—А., ESK stiidit's of pyrrole polymers: evidence for bipolarons, <.Phys. H<;v.»t 1983, v. –Т 28, p. 2140. R. –Ы. –Т–Є–Ї–µ—Ж–Ї–Є–є. –С–Ш–°–Я–Ш–Ш–Ю–† вЙИ –і–љ—А–∞–Ї–Њ–≤—Б–Ї–Є–є —Б–њ–Є–љ–Њ—А –≤ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–Є, –≥–і–µ –Љ–∞—В—А–Є—Ж–∞ —Г—М –і–Є–∞–≥–Њ–љ–∞–ї—М–љ–∞ (—Б–Љ. –Ф–Є—А–∞–Ї–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ]. –С. —П–≤–ї—П–µ—В—Б—П —З–µ—В—М–≥—АвХ¶—Е–Ї–Њ–Љ–њ–Њ–њ–µ–љ—В–љ—Л–Љ —Б—В–Њ–ї–±—Ж–Њ–Љ вЙИ –њ–∞—А–Њ–є –і–≤—Г—Е–Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–≤—Л—Е —Б—В–Њ–ї–±—Ж–Њ–≤:
*
–≥–і–µ –Є–љ–і–µ–Ї—Б—Л –∞ (–љ–µ—И—В—А–љ—Е–Њ–љ–∞–љ–љ—Л–є) –Є —А' (—И—В—А–Є—Е–Њ–≤–∞–љ–љ—Л–є) –њ—А–Њ–±–µ–≥–∞—О—В –Ј–љ–∞—З–µ–љ–Є—П 1 –Є 2. –Э–Њ –Њ—В–љ–Њ—И–µ–љ–Є—О –Ї –≥—А—Г–њ–њ–µ
—В—АвХ¶—Е–Љ–µ—А–љ—Л—Е –љ—А–∞—Й–µ–љ–љ–Є (—А–∞ –Є —Г^ —П–≤–ї—П—О—В—Б—П –Њ–±—Л—З–љ—Л–Љ–Є –Љ–Є, –њ—А–µ–Њ–±—А–∞–Ј—Г—О—Й–Є–Љ–Є—Б—П –њ–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—О /J1''3
–°–Ю —Б–њ–Є–ї–Њ–Љ 1/–∞. –†–∞–Ј–ї–Є—З–Є–µ –Љ–µ–ґ–і—Г –љ–Є–Љ–Є –њ—А–Њ—П–≤–ї—П–µ—В—Б—П –њ—А–Є –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П—Е –Ы–Њ—А–µ–љ—Ж–∞: —Б–њ–Є–љ–Њ—А—Л —Д –Є —Е –њ—А–µ–Њ–±—А–∞–Ј—Г—О—В—Б—П –Ї–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П–Љ, –Ї-—А—Л–µ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ —Б–Њ–њ—А—П–ґ–µ–љ—Л –і—А—Г–≥ –і—А—Г–≥—Г, –њ–Њ —В. –љ. –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П–Љ D^ !*вИЩ °' –њ />^°' *^' –≥—А—Г–њ–њ—Л –Ы–Њ—А–µ–љ—Ж–∞. –Т –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є –њ–Њ–ї—П –С. —Г–і–Њ–±–љ—Л –і–ї—П –µ–і–Є–љ–Њ–Њ–±—А–∞–Ј–љ–Њ–≥–Њ –Њ–њ–Є—Б–∞–љ–Є—П –Љ–∞—Б—Б–Є–≤–љ—Л—Е –Є –±–µ–Ј–Љ–∞—Б—Б–Њ–≤—Л—Е —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Є—Е —З–∞—Б—В–Є—Ж —Б–Њ —Б–њ–Є–љ–Њ–Љ 1/2.
–Ы–Є—В.: IJ —Б —А —Б —Б —В –Њ —Ж –Ї –Ї –Є –С. –Т., .11 –Є —Д —И –Є —Ж –Х. –Ь., II –Є-—В –∞ —А –≤ —Б –Ї ir ii –Ы. –Я., –Ъ–њ–∞–љ—В–Њ–љ–∞–ї –Њ.: i –µ–Ї—В –≥ >–њ –і–Є–љ–∞–Љ–Є–Ї–∞, 2 –Є:—Й., –Ь., 11)–Э(): –С —М вХ¶ —А –Ї –Њ –љ –Ф –ґ. –Ф-, –Ф —А –µ –ї –ї –°. –Ф., –†–µ–ї—П—В–Є-—А–Є—Б—В—Б–љ–∞–Љ —М'–≤–∞–љ—В–Њ–Є–∞—П —В–µ–Њ—А–Є–Є, –њ–Њ—А, i; –∞–љ–≥.:1., –≥, t, M,, 1S*7S.
–Р. –Ш. –Ю–Ї—Б–∞–Ї. –С–Ш–Ґ {–±–Є—В, bit) (<JT –∞–љ–≥–ї, binary вЙИ –і–≤–Њ–Є—З–љ—Л–є –Є digit вЙИ
–Ј–љ–∞–Ї, —Ж–Є—Д—А–∞) вЙИ –µ–і–Є–љ–Є—Ж–∞ –Ї–Њ–ї-–≤–∞ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є –≤ –і–≤–Њ–Є—З–љ–Њ–є —Б–Є—Б—В–µ–Љ–µ. –Ъ–Њ–ї-–≤–Њ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є
–њ - Iog2 N –±–Є—В,
–≥–і–µ N вЙИ —З–Є—Б–ї–Њ —А–∞–≤–љ–Њ–љ—Б—А–Њ—П—В–љ—М–≥—Е —Б–Њ–±—Л—В–Є–Є –њ–ї–Є —Б–Њ—Б—В–Њ—П–љ–Є–є. —Б—А–µ–і–Є –Ї-—А—Л—Е —Б –њ–Њ–Љ–Њ—Й—М—О –њ —Б–Њ–Њ–±—Й–µ–љ—В–њ! —В–Є–њ–∞ «–і–∞ вЙИ –љ–µ—В» –Љ–Њ–ґ–љ–Њ –≤—Л–і–µ–ї–Є—В—М –Њ–Є—А–µ–і–µ–ї. —Б–Њ—Б—В–Њ—П–љ–Є–µ. –Ґ–∞–Ї, —З—В–Њ–±—Л —Г–Ї–∞–Ј–∞—В—М –Ї. -–ї. –Ї–ї–µ—В–Ї—Г –Є–Ј fi4 –Ї–ї–µ—В–Њ–Ї —И–∞—Е–Љ–∞—В–љ–Њ–є –і–Њ—Б–Ї–Є, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –љ = –Т –±–Є—В –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є (–љ–µ—А—Е–љ—П—П –Є–ї–Є –љ–Є–ґ–љ—П—П –њ–Њ–ї–Њ–≤–Є–љ–∞ –і–Њ—Б–Ї–Є, –ї–µ–≤–∞—П –Є–ї–Є –њ—А–∞–≤–∞ —З–∞—Б—В—М –µвХ¶ –Є —В. –і.}. –Я–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М –Є–Ј 8 –С. –љ–∞–Ј. –± –∞ –Є —В –Њ –Љ.
–С–Ш–§–£–†–Ъ–Р–¶–Ш–ѓ (–њ–Њ–≤–Њ–і–Є—В, bifurcalio, –Њ—В –ї–∞—В. bifnr-cua вЙИ —А–≤–Ј–і–≤–Њ–µ—И—И–њ) вЙИ –њ—А–Є–Њ–±—А–µ—В–µ–љ–Є–µ –љ–Њ–≤–Њ–≥–Њ –Ї–∞—З–µ—Б—В–≤–∞ –і–≤–Є–ґ–µ–љ–Є—П–Љ–Є –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –њ—А–Є –Љ–∞–ї–Њ–Љ –Є–Ј–Љ–µ–љ–µ–љ–Є–Є –µвХ¶ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤. –Ґ1. —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –њ–µ—А–µ—Б—В—А–Њ–є–Ї–µ —Е–∞—А–∞–Ї—В–µ—А–∞ –і–≤–Є–ґ–µ–љ–Є—П —А–µ–∞–ї—М–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л (—Д–Є–Ј., —Е–Є–Љ; –Є —В. –і.). –Ю—Б–љ–Њ–љ—Л —В–µ–Њ—А–Є–Є Ij. –Ј–∞–ї–Њ–ґ–µ–љ—Л –Ы. llyairxapc (–Э. Poincare) –Є –Р. –Ь . –Ы—П—В–≥—Г–љ–Њ–љ—Л–Љ –≤ –љ–∞—З. 20 –љ., ;*–∞—В–µ–Љ —Г—В–∞ —В–µ–Њ—А–Є–Є –±—Л–ї–∞ —А–∞–Ј–≤–Є—В–∞ –Р, –Р. –Р–љ–і—А–Њ–њ–Њ–≤—Л–Љ –Є –µ–≥–Њ —Г—З–µ–љ–Є–Ї–∞–Љ–Є. –Ч–љ–∞–љ–Є–µ –Њ—Б–љ–Њ–≤–љ—Л—Е –С. –њ–Њ–Ј–≤–Њ–ї—П–µ—В —Б—Г—Й–µ—Б—В–Є–µ–љ–љ–Њ –Њ–±–ї–µ–≥—З–Є—В—М –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ –Ї–Њ–љ–Ї—А–µ—В–љ—Л—Е —Д–Є–Ј. —Б–Є—Б—В–µ–Љ, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є –њ—А–µ–і—Б–Ї–∞–Ј–∞—В—М –њ–∞—А–∞–Љ–µ—В—А—Л –љ–Њ–≤—Л—Е –і–≤–Є–ґ–µ–љ–Є–Є, –≤–Њ–Ј–љ–Є–Ї–∞—О–ї—Ж—В—Е –ї –Љ–Њ–Љ–µ–љ—В –њ–µ—А–µ—Е–Њ–і–∞, –Њ—Ж–µ–љ–Є—В—М –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Њ–±–ї–∞—Б—В–Є –Є—Е —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П –љ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є –Є —В. –і. –≠—В–Њ –Њ—В–љ–Њ—Б–Є—В—Б—П –Ї–∞–Ї –Ї —Б–Є—Б—В–µ–Љ–∞–Љ —Б —Б–Њ—Б—А–µ–і–Њ—В–Њ—З–µ–љ–љ—Л–Љ–Є –њ–∞—А–∞–Љ–µ—В—А–∞–Љ–Є, —В–∞–Ї –Є –Ї —Б–Є—Б—В–µ–Љ–∞–Љ —Б —А–∞—Б–њ—А–µ–і–µ–ївХ¶–љ–љ—Л–Љ–Є –њ–∞—А–∞–Љ–µ—В—А–∞–Љ–Є.
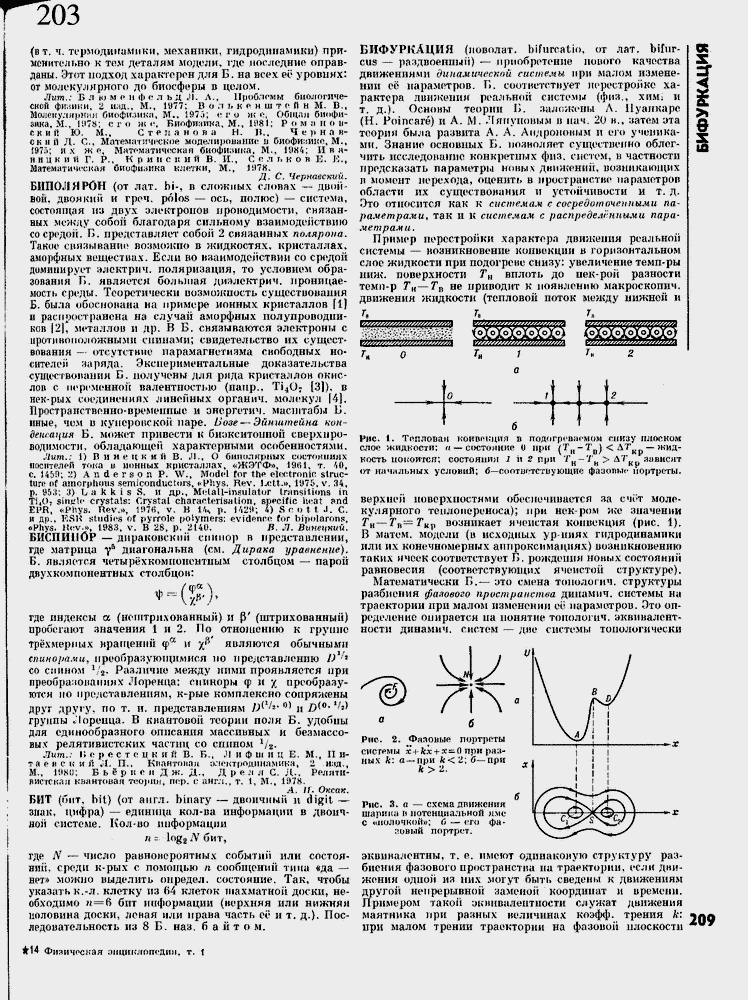
–Я—А–Є–Љ–µ—А –њ–µ—А–µ—Б—В—А–Њ–є–Ї–Є —Е–∞—А–∞–Ї—В–µ—А–∞ –і–≤–Є–ґ–µ–љ–Є—П —А–µ–∞–ї—М–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л вЙИ –≤–Њ–Ј–љ–Є–Ї–љ–Њ–≤–µ–љ–Є–µ –Ї–Њ–љ–≤–µ–Ї—Ж–Є–Є –≤ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–Њ–Љ —Б–ї–Њ–µ –ґ–Є–і–Ї–Њ—Б—В–Є –њ—А–Є –њ–Њ–і–Њ–≥—А–µ–≤–µ —Б–љ–Є–Ј—Г: —Г–≤–µ–ї–Є—З–µ–љ–Є–µ —В–µ–Љ–њ-—А—Л –љ–Є–ґ. –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ґ–∞ –≤–њ–ї–Њ—В—М –і–Њ –љ–µ–Ї-—А–Њ–љ —А–∞–Ј–љ–Њ—Б—В–Є —В–µ–Љ–њ-—А –Ґ–љвЙИ–Ґ–њ –љ–µ –њ—А–Є–≤–Њ–і–Є—В –Ї –њ–Њ—П–≤–ї–µ–љ–Є—О –Љ–∞–Ї—А–Њ—Б–Ї–Њ–њ–Є—З. –і–≤–Є–ґ–µ–љ–Є—П –ґ–Є–і–Ї–Њ—Б—В–Є (—В–µ–њ–ї–Њ–≤–Њ–є –њ–Њ—В–Њ–Ї –Љ–µ–ґ–і—Г –љ–Є–ґ–љ–µ–є –Є
–Ю
–Њ
–†–Є—Б. 1. –Ґ–µ–њ–ї–Њ–≤–∞—П –Ї–Њ–љ–≤–µ–љ—Ж–Є—П –≤ –њ–Њ–і–Њ–≥—А–µ–≤–∞–µ–Љ–Њ–Љ —Б–љ–Є–Ј—Г –њ–ї–Њ—Б–Ї–Њ–Љ —Б–ї–Њ–µ –ґ–Є–і–Ї–Њ—Б—В–Є: «вЙИ—Б–Њ—Б—В–Њ—П–љ–Є–µ 0 –њ—А–Є (–Ґ[(-7'–≤) < –Ы–Ґ вЙИ –ґ–Є–і-
–Ї–Њ—Б—В—М –њ–Њ–Ї–Њ–Є—В—Б—П; —Б–Њ—Б—В–Њ—П–љ–Є—П 1 –Є 2 –њ—А–Є –Ґ–Э-7–Э
–Ф–У–У –Ј–∞–≤–Є—Б—П—В –Ї —А
–Њ—В –љ–∞—З–∞–ї—М–љ—Л—Е —Г—Б–ї–Њ–≤–Є–є; –±вЙИ–µ–Њ–Њ—В–Є–Њ—В—Б—В–≤—Г–Ї—П—Й—В—Б —Д–∞–Ј–Њ–≤—Л–µ –њ–Њ—А—В—А–µ—В—Л.
–≤–µ—А—Е–љ–µ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—П–Љ–Є –Њ–±–µ—Б–љ–µ—З–Є–≤–∞–Њ—В—Б—П –Ј–∞ —Б—ЗвХ¶—В –Љ–Њ–ї–µ–Ї—Г–ї—П—А–љ–Њ–≥–Њ —В–µ–њ–ї–Њ –њ–µ—А–µ–љ–Њ—Б–∞); –њ—А–Є –љ–µ–Ї-—А–Њ–Љ –ґ–µ –Ј–љ–∞—З–µ–љ–Є–Є –Ґ–љвЙИ–У–≤вЙИ–У–Ъ() –≤–Њ–Ј–љ–Є–Ї–∞–µ—В —П—З–µ–Є—Б—В–∞—П –Ї–Њ–љ–≤–µ–Ї—Ж–Є—П (—А–Є—Б. 1). –Т –Љ–∞—В–Њ–Љ, –Љ–Њ–і–µ–ї–Є (–≤ –Є—Б—Е–Њ–і–љ—Л—Е —Г—А-—И—И—Е –≥–Є–і—А–Њ–і–Є–љ–∞–Љ–Є–Ї–Є –Є–ї–Є –Є—Е –Ї–Њ–љ–µ—З–љ–Њ–Љ–µ—А–љ—Л—Е –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є—П—Е) –≤–Њ–Ј–љ–Є–Ї–љ–Њ–≤–µ–љ–Є–Є! —В–∞–Ї–Є—Е –Є—З–Њ—Б–Ї —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –С. —А–Њ–ґ–і–µ–љ–Є—П –љ–Њ–≤—Л—Е —Б–Њ—Б—В–Њ—П–љ–Є–є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П (—Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е —П—З–µ–Є—Б—В–Њ–є —Б—В—А—Г–Ї—В—Г—А–µ). –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Я.вЙИ —Н—В–Њ —Б–Љ–µ–љ–∞ —В–Њ–њ–Њ–ї–Њ–≥–Є—З. —Б—В—А—Г–Ї—В—Г—А—Л —А–∞–Ј–±–Є–µ–љ–Є—П —Д–∞–Ј–Њ–≤–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ –і—И—И–Љ–Є—З. —Б–Є—Б—В–µ–Љ—Л –љ–∞ —В—А–∞–µ–Ї—В–Њ—А–Є–Є –њ—А–Є –Љ–∞–ї–Њ–Љ –Є–Ј–Љ–µ–љ–µ–љ–Є–Є –µвХ¶ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤. –≠—В–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –Њ–њ–Є—А–∞–µ—В—Б—П –њ–∞ –њ–Њ–љ—П—В–Є–µ —В–Њ–њ–Њ–ї–Њ–≥–Є—З. —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ—Б—В–Є –і–Є–љ–∞–Љ–Є—З. —Б–Є—Б—В–µ–Љ вЙИ –і–љ–µ —Б–Є—Б—В–µ–Љ—Л —В–Њ–њ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є
–∞
–∞
–†–Є—Б. 2. –§–∞–Ј–Њ–Є—Л–µ –њ–Њ—А—В—А–µ—В—Л
—Б–Є—Б—В–µ–Љ—Л *-[ –є—Е + —Е = 0 –њ—А–Є —А–∞–Ј–љ—Л—Е k; –∞вЙИ–њ—А–Є k<2; –±вЙИ–њ—А–Є ft >2,
–†–Є—Б. 3. –∞ вЙИ —Б—Е–µ–Љ–∞ –і–≤–Є–ґ–µ–љ–Є—П —И–∞—А–Є–Ї–∞ –њ–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ —Б «–њ–Њ–ї–Є—З–љ–Њ–є»; –± вЙИ –µ–≥–Њ —Д–∞-–њ–Њ—А—В—А–µ—В.
—Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ—Л, —В. –†., –Є–Љ–µ—О—В –Њ–і–Є–љ–∞–Ї–Њ–≤—Г—О —Б—В—А—Г–Ї—В—Г—А—Г —А–∞–Ј–±–Є–µ–љ–Є—П —Д–∞–Ј–Њ–≤–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ –љ–∞ —В—А–∞–µ–Ї—В–Њ—А–Є–Є, –µ—Б.–њ–Ї –і–≤–Є–ґ–µ–љ–Є—П –Њ–і–љ–Њ–є –Є—П –љ–Є—Е –Љ–Њ–≥—Г—В –±—Л—В—М —Б–≤–µ–і–µ–љ—Л –Ї –і–≤–Є–ґ–µ–љ–Є—П–Љ –і—А—Г–≥–Њ–є –љ–µ–њ—А–µ—А—Л–≤–љ–Њ–є –Ј–∞–Љ–µ–љ–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В –Є –≤—А–µ–Љ–µ–љ–Є. –Я—А–Є–Љ–µ—А–Њ–Љ —В–∞–Ї–Њ–є —Н–Ї–љ–Є–≤–∞–ї–µ–њ—В–њ–Њ—Б—В–Є —Б–ї—Г–ґ–∞—В –і–≤–Є–ґ–µ–љ–Є—П –Љ–∞—П—В–љ–Є–Ї–∞ –њ—А–Є —А–∞–Ј–љ—Л—Е –≤–µ–ї–Є—З–Є–љ–∞—Е –Ї–Њ—Н—Д—Д. —В—А–µ–љ–Є—П k: –њ—А–Є –Љ–∞–ї–Њ–Љ —В—А–µ–љ–Є–Є —В—А–∞–µ–Ї—В–Њ—А–Є–Є –љ–∞ —Д–∞–Ј–Њ–≤–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є
–µ
—И
209
–§–Є–Ј–Є—З–µ—Б–Ї–∞—П —Н–љ—Ж–Є–Ї–ї–Њ–њ–µ–і–Є–Є, –≥. \
")
}


