1tom - 0099.htm

1
с о
о.
ш
имеют по-
Д/АЛ- о-, 1~, 0~ (запрещены переходы 0 -- 0,
Г Г
¹/г --∙ ¹/а)« Матричные элементы \\ Ve ^и \\ ^а
j J
рядок малости (VNJC)* Для матричных элементов, содержащих величину г, естественно ожидать малости порядка pR\\ti^£₍bR\\'kc. Однако JTO справедливо только для уникальных переходов. Для остальных матричных элементен в случае, когда заряд ядра Z удовлетворяет условию § = (Ze²//?£₀) ^> 1, кулоыовские эффекты приводят к возрастанию волновой ф-ции электрона внутри ядра, вследствие чего эти матричные элементы имеют порядок малости Z/137, а но pRfk. Условие \ ^> 1 выполняется для большинства р-персходов.
С ростом порядка запрета кол-во матричных элементов, определяющих вероятность перехода, увеличивается и трудность анализа эксперим. данных возрастает; при атом сами матричные Элементы убывают по порядку величины. Правила отбора при р-мерехо-дах п-го порядка запрета: Лл ≈ ( ≈ 1)^п, А/ <; п для обычных переходов н^я-|-1 для уникальных переходов.
С ростом п и уменьшением матричных элементов величина /Т¹, возрастает. Хотя диапазон е╦ изменения
уже, чем для Т*; , он вс╦ же очень велик; поэтому принято характеризовать ^-переходы величиной Jg f?¹ i/
(табл. 2).
В сочетании с правилами отбора анализ величин /7*!, позволяет определить неизвестные значения ядер-
ных спинов и ч╦тностей, т. е. является одним из важ-ны-V методов ядерной спектроскопии. Т. к. величины /7Y непосредственно связаны с матричными элемен-
тами ^-переходов, то они содержат информацию о ядерной структуре.
T;i Г> л. 3. ≈ Правила отбора для pi-переходов различных типов


Тип перехода	Правила отбора	^	«^,.
Разрешенные
плт^удп╦нныс . . .	1Дл=ч-^%1	Г: \ 1 .1 1 ! Т
Запрещ╦нные
иерииго запргта . .	ДГ=1,0,	7,5±i .5
	Дл = ≈ 1
унинальньн: лсрвп-
гп запрети .....	L^f ≈ 2,
	Дл = ≈ 1		8 , 5±fi, 7
DTOjuirn запргта . .	Д/≈ '2.
	Дя≈ -ь 1	12, lit. 0
уникллыпйе JITOJJO-
го ;1мпргта . . . . .	Д ' = 3,
	Д.ТГ- + 1		11,7±О.Э
Tii"'Tb(T<i амгфгта . .	AT ⁼ -1	18 2-0
униь'^лышо третье-	А"-'
го iiUUpi'Til . . . . .	Дл^-1		15.2 (<*К)
чс'ш╦ртоги запрета	Л / -- ^ri ,
	ЛЯ- 1 1	22,7 ('"In)

194
экспериментально исследуются, как правило, с помощью бета-сш'ктромет.рив. В случае разреш╦нных переходов р-спсктры описываются ниранге-нием:
N(£)dG ~ F(Z> g)pff(gb~fi)*df;. (12)
Для исследования р-спсктров удобно пользоваться т. н. г р а ф и к а м и 1х ю р н. к-рые изображают эалисимость
величины /C"_-[-V(^r)//'(/2, с⁽;)/^]'^/3 от t. Для раз-реш╦нных лсрсходон график Кюри имеет вид отрезка прямо», uopeceKaioiueii ось абсцисс в точке $ = £₀(рис, 4), Отличие; перехода от разреш╦нного приводит к нарушению линейности. Б ста-спектры запрещенных переходов могут значительно отличаться от paapouieir-ны\\ спектров из-за наличия зависяш,их от энергии членов в матричном члсчснто. Этот оффокт обычно учитывается введением в правую часть выражения (12J зависящего от энергии множителя S (Л.) (т. н. спек т-
рального формфактор а). Для уникальных переходов 1-го запрета (в пренебрежении кулоновскими
эффектами):
S~[(£*--m_ec)2 + (£₀-£)*], (13) Уникальные переходы n-го запрета часто
a
зуют не величинами ется ф-лоп вида (96),
к
8
7 6 Б U 3 2 1
f_nTi , где
характери/└ определя-
выражение
О 200 400 600 800 100 3DO 500 700 £,кэВ
К 1.5
подынтегральное
1,0
0,5
О
О 2 4
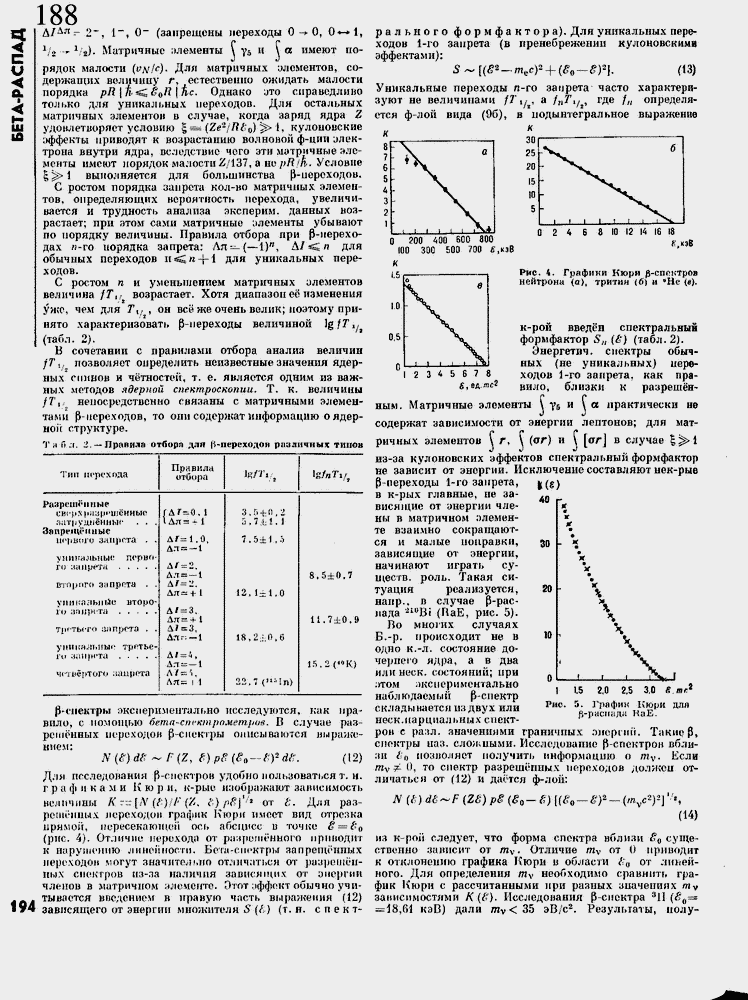
Рис. 4. Графини Кюри
нейтрона (а), тритин (б) и «Не (в).
I 2 3 4 5 6 7 8
к-рои введ╦н спектральный формфактор S_n (╗) (табл. 2).
Энергетич. спектры обычных (не уникальных) переходов 1-го запрета, как пра-е,едтс< вило, близки к разреш╦н-
ным. Матричные элементы \\ у_а и \\ а практически не содержат зависимости от энергии лептонов; для матричных элементов \\ Л \\ (®г] и \\ [<тг] в случае 1^-1
из-за кулоновских эффектов спектральный формфактор не зависит от энергии. Исключение составляют нек-рые Р-переходы 1-го запрета, в к-рых главные, не зависящие от энергии чле~ ны в матричном элементе взаимно сокращаются и малые поправки, зависящие or анергии, начинают играть существ, роль. Такая ситуация реализуется, напр., в случае р-рас-лада ^2i(>Bi (ПаЕ, рис. 5). Во многих случаях Б.-р. происходит не в одно к.-л. состояние дочернего ядра, а в два или неск. состояний; при ;ш>м экспериментально наблюдаемый р-спектр складывается ив двух или неск. пар ц нал ь н ы х с нект-
10
ж It
∙ ф
L ж
* к
\
J
I 15
3,0
2,0 2.5
Рис. 5. График Нюри для
6-риспади НаЕ. '
рои с ра;1л. значениями граничных nuopmii. Такие спектры паз. сложными. Исследование р-спсктрон вблизи £₀ позволяет получить информацию о m_v. Если m_v f- 0, то спектр разреш╦нных переходов должен отличаться от (12) и дастся ф-лой:
(14)
из к-poii следует, что форма спектра вблизи £$ существенно зависит от tn_v. Отличие пг\\ от 0 приводит к отклонению графика Кюри и области £└ от лишенного. Для определения m_v необходимо сравнить график Кюри с рассчитанными при разных значениях m_vзанисимостлми К (8). Исследовании р-смоктра ³11 (^₀ = =18,61 кэС) дали m_v < 35 эВ/с². Результаты, полу-
") }