скорости С/≈ const (пограничный слой на продольно обтекаемой бесконечной плоской пластине). Т.к. в рассматриваемом течении нет к.-л. характерной длины, то профили скорости v в автомодельном пограничном слое в разл. поперечных сечениях х = const подобны друг Другу и в безразмерных переменных представляются универсальной ф-цией и/£/=<р(<//6), где у ≈ расстояние по нормали к пластине, 6 ≈ толщина пограничного слоя. Безразмерная ф-ция тока /(г;) в автомодельном пограничном слое удовлетворяет обыкновенному дифференц. ур-нию
АВТОМОДЕЛЬНОСТЬ ≈ особая симметрия физ. системы, состоящая в том, что изменение масштабов независимых переменных может быть скомпенсировано преобразованием подобия др. динамич. переменных. А. приводит к эфф. сокращению числа независимых переменных. Напр., если состояние системы характеризуется ф-цией и(х, /), где х ≈ координата, t ≈ время, то условие инвариантности относительно изменения масштабов xf~kxr t' = lt и преобразования подобия таково:
а
x, It),
с граничными условиями /=0, /' = 0 при т]^0 и /' = 1 при т) =оо. Здесь а, р ≈ нск-рые постоянные, а Т] ≈ безразмерная автомодельная переменная, пропорциональная у/&. Аналогичные Л. т. возможны и в пограничном слое, возникающем ири свободной (естественной) конвекции,
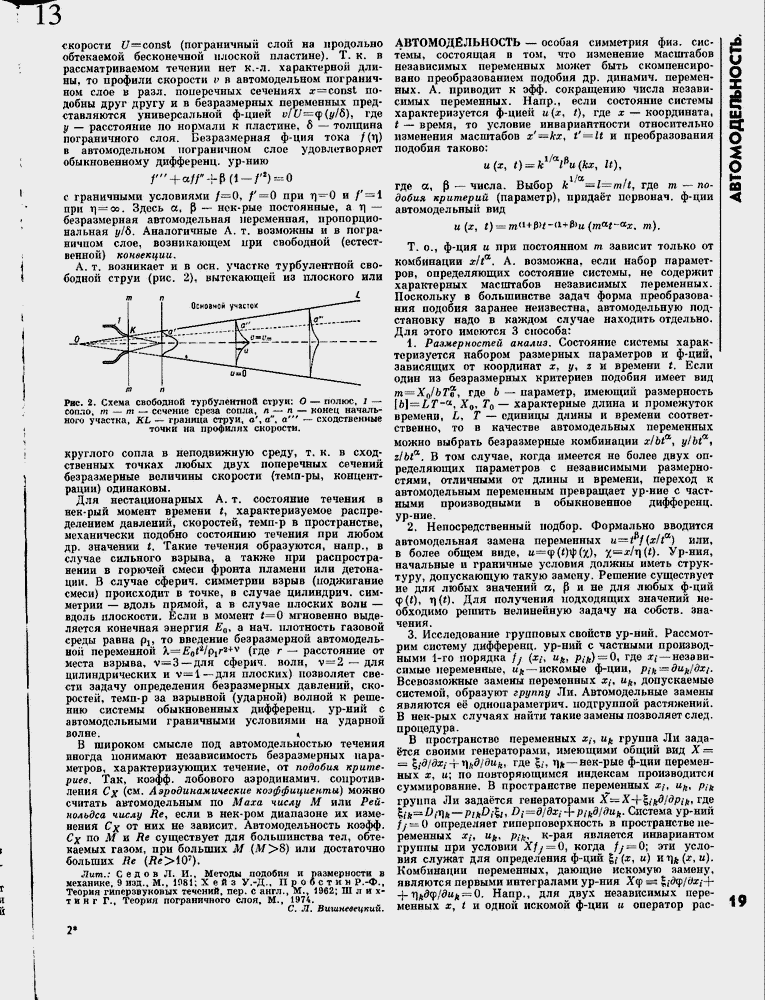
А. т. возникает и в осн. участке турбулентной свободной струи (рис. 2), вытекающей из плоского или
'
Рис. 2. Схема свободной турбулентной струи: О ≈ полюс, 1 ≈ сопло, т ≈ т ≈ сечение среза сопла, п ≈ п ≈ нонец начального участка, KL ≈ граница струи, а', а", а"' ≈ сходственные
точки на профилях скорости.
круглого сопла в неподвижную среду, т. к. в сходственных точках любых Двух поперечных сечений безразмерные величины скорости (темп-ры, концентрации) одинаковы.
Для нестационарных А. т. состояние течения в нек-рый момент времени г, характеризуемое распределением давлений, скоростей, темп-р в пространстве» механически подобно состоянию течения при любом др. значении t. Такие течения образуются, напр., в случае сильного взрыва, а также при распространении в горючей смеси фронта пламени или детонации. В случае сферич. симметрии взрыв (иоджигание смеси) происходит в точке, в случае цилиндрич. симметрии ≈ вдоль прямой, а в случае плоских волн ≈ вдоль плоскости. Если в момент f=0 мгновенно выделяется конечная энергия £"<,, а нач. плотность газовой среды равна pls то введение безразмерной автомодель-нон переменной A,=£o*a/Pi''a+v (гДе г ~^ расстояние от места взрыва, v=3≈ для сферич. волн, v=2 ≈ для цилиндрических и v=l≈ для плоских) позволяет свести задачу определения безразмерных давлений, скоростей, темп-р за взрывной (ударной) волной к решению системы обыкновенных дифференц. ур-ний с автомодельными граничными условиями на ударной волне . *
В широком смысле под автомодельностью течения иногда понимают независимость безразмерных параметров, характеризующих течение, от подобия критериев. Так, коэфф. лобового аэродинамич. сопротивления Сх (см- Аэродинамические коэффициенты) можно считать автомодельным по Маха числу М или Рей-нольдса числу Re, если в нек-ром диапазоне их изменения Сх от них не зависит. Автомодельность коэфф. Сх по М и Re существует для большинства тел, обтекаемых газом, при больших М (М >8) или достаточно больших Не
Лит.; Седов Л. И., Методы подобия и размерности в механике, 9 изд., М., 1081; X е и з У, -Д., Пробстин Р.-Ф., Теория гиперзвуковых течений, пер. с англ., М., 1962; Ш л и х-тинг Г.* Теория пограничного слоя, М,, 1974,
С. Л. Вишневецкий.
где а, р ≈ числа. Выбор k ' ≈l≈m/t, где т ≈ подобия критерий (параметр), прида╦т первонач. ф-ции автомодельный вид
и(х, *) = m<i+j3>/-(i+e>u(maf-aa;, т).
Т. о., ф-ция и при постоянном т зависит только от
комбинации x/ta. А. возможнат если набор параметров, определяющих состояние системы, не содержит характерных масштабов независимых переменных. Поскольку в большинстве задач форма преобразования подобия заранее неизвестна, автомодельную подстановку надо в каждом случае находить отдельно. Для этого имеются 3 способа:
1. Размерностей анализ. Состояние системы характеризуется набором размерных параметров и ф-ций, зависящих от координат х, у, z и времени t. Если один из безразмерных критериев подобия имеет вид
т=Х0/Ь71?, где Ъ ≈ параметр, имеющий размерность [й] = //Г-а, XG, Г0 ≈ характерные длина и промежуток времени, L, Т ≈ единицы длины и времени соответственно, то в качестве автомодельных переменных
можно выбрать безразмерные комбинации x/btat ylbt^-,
zlbta. В том случае, когда имеется не более двух определяющих параметров с независимыми размерностями, отличными от длины и времени, переход к автомодельным переменным превращает ур-ние с частными производными в обыкновенное дифференц. ур-ние,
2. Непосредственный подбор. Формально вводится
автомодельная замена переменных u=rf(xltctr) или, в более общем виде, и=ф(01РОс)> X≈ Х//Л (О- Ур-ния, начальные и граничные условия должны иметь структуру, допускающую такую замену. Решение существует не для любых значений а, р и не для любых ф-ций ф(£), K\\(t), Для получения подходящих значений необходимо решить нелинейную задачу на собств. значения.
3. Исследование групповых свойств ур-ний. Рассмотрим систему дифференц. ур-ний с частными производными 1-го порядка fj (л:/, Ufa Pijt) = 0, где я,- ≈ независимые неременные, «й ≈ искомые ф-ции, р/А ≈ du^/dxi. Всевозможные замены переменных лг/, м^, допускаемые системой, образуют группу Ли, Автомодельные замены являются ее одноиараметрич. подгруппой растяжений. В нек-рых случаях найти такие замены позволяет след. процедура.
В пространстве переменных #/, и^ группа Ли зада╦тся своими генераторами, имеющими общий вид X ≈ = £i-3/#Bi'-r11fc0/0ufe. где £ь ч>≈ нек-рые ф-ции переменных х, и; по повторяющимся индексам производится суммирование. В пространстве переменных я/, и^, р/л
группа Ли зада╦тся генераторами J?=X-f j-^/dp^, где tib=&Mk ≈ PtbDfai Di=djdxi-]-pihdjduh. Система ур^ний /у=^0 определяет гиперповерхность в пространстве переменных tf/t Ufc, р; ь, к-рая является инвариантом группы при условии Х/у = 0, когда /у = 0; эти условия служат для определения ф-ций £,-(#, и) ит|^(лг,и). Комбинации переменных, дающие искомую замену, являются первыми интегралами ур-ния Хф = Е/^Ф/йя1 + + т] д0ф/дид ≈ 0. Напр . , для двух независимых переменных xt t и одной искомой ф-ции и оператор рас-
и
о
X л
ш Ч О
О
19
")
}


