1tom - 0020.htm
Ш
-О
и о
устраняя олижаитпие к центру один-два светлых ди-Фракц, кольца.
В спектроскопии А. облегчает обнаружение сателлитов спектральных линии, в астрономии ≈ разрешение двойных зв╦зд С сильно различающейся видимой яркостью.
Лит.: М а р « ш а л ь А., Ф р а и г г> н М., Структура огг-тич<.;ск(зго изображения, ш'р. с франц., М-, Ш>4.
Г. Г, Слюсарев>
АПОСТЙЛЬБ (ас-б) ≈ устаревшая единица яркости; 1 асб=1/я-1С)-4 стштьб=0,ЗШ кд/м2-10~4 ломбер т. АПОХРОМАТ ≈ оптич. система, отличающаяся от ахромата более совершенным испранлением хроматических аберраций, и в первую очередь испранлепьем вторичного спектра, к-рый проявляется в несовпадении плоскости резкого изображения для лучей пек-рои длины волны £3 с совмещенными в результате ахроматина-ции изображениями для лучоп длин волн KL и Я2 при A-i <А,П<Х2- Радикальным средством для аиохромати-вации линзовых оптич. систем является применении пары оптич, материалов, обладающих существенно раял. дисперсиями п^ ≈ п? и равными или близкими по чисзначениям относит, частными дисперсиями _/(п^ ≈ Лд ). Такими свойствами обладает, в
частности, пара: флюорит (CaF2) и стекло из группы «особый флинт». А. по сравнению с ахроматами либо применяются в более широкой области спектра, либо при одинаковой области спектра создают более совершенное изображение. Наиб, широко А. используются it качестве объектинов для микроскопов.
Лит. см. при ст, Айеррцции оптических систем.
А. П. Грамматпп,
АППАРАТНАЯ ФУНКЦИЯ ≈характеристика лилейного измерит, устройства, устанавливающая свяиь измеренной величины па выходе устройства с истинным значенном этой величины на его входе. Наиб, часто с помощью А. ф. характеризуют спектральные приборы. Математически А. ф. определяется из ур-ния
ленным
а
≈х'} ф (xr)
(*)
где / (х) ≈ измеренное распределение фнз. величины, <р(х] ≈ истинное распределение, а(х] ≈∙ А. ф. Во мн. исследованиях возникает задача вычисления истинного распределения ф (х) по измеренному / (х) и известной А. ф. Эта задача сводится к решению интегрального ур-ния (*) относительно ф-ции ф (j). Для решения ур-пия
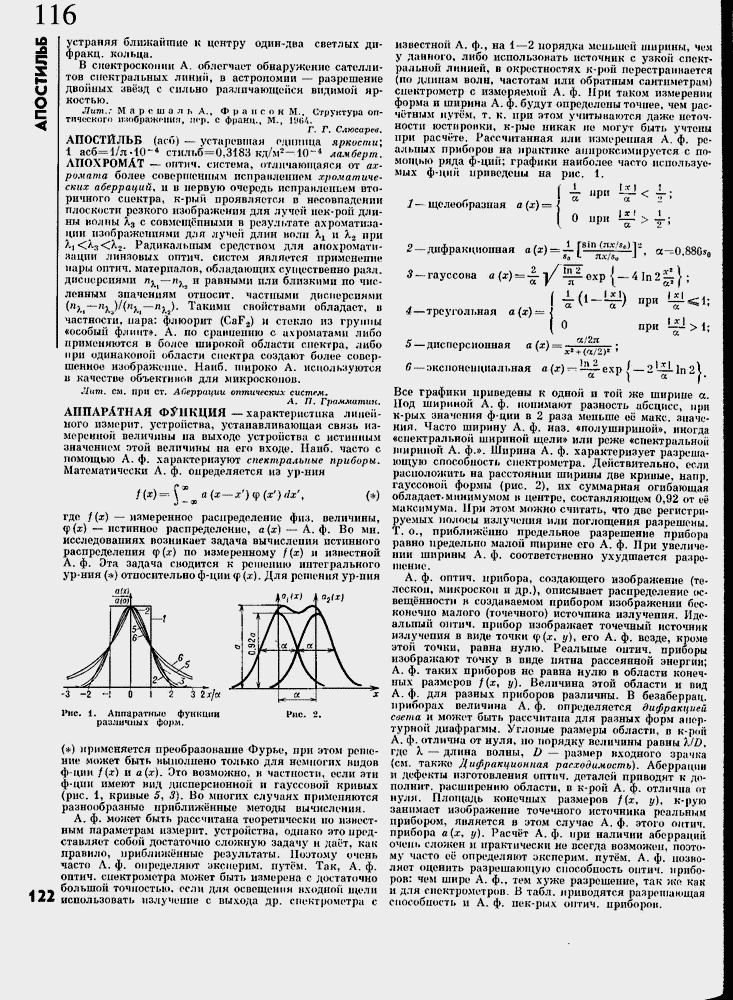
Апгтараткыс функции рааличных форм.
Рис. 2.
122
(*) применяется преобразование Фурье, при этом решение может быть ныполнено только для немногих видов ф-ции /(.г) и а (х). Это возможно, в частности, если эти ф-ции имеют вид дисперсионной и гауссовой кривых (рис. 1, кривые 5, 3). Во многих случаях применяются разнообразные приближ╦нные методы вычисления.
А. ф. может быть рассчитана теоретически по манжетным параметрам измерит, устройства, однако ато представляет собой достаточно сложную задачу и да╦т, как правило, приближ╦нные результаты. Поэтому очень часто А. ф. определяют эксиирим, пут╦м. Так, А. ф. оптич. спектрометра может быть измерена с достаточно большой точностью, ос л и длн освещения их одной щели использовать излучение с выхода др, спектрометра с
известной А. ф., на 1≈2 порядка меньшой ширины, чем у данного, либо использовать источник с узкой спектральной линией, в окрестностях к-рой перестраивается (по длинам волн, частотам или обратным сантиметрам) спектрометр с измеряемой А. ф. При таком измерении форма и ширина А. ф. будут определены точнее, чем расчетным пут╦м, т. к. при этом учитываются даже поточности юстироики, к-рые никак не могут быть учтены при расч╦те. Рассчитанная или измеренная А. ф. реальных приборов на практике аппроксимируется с помощью ряда ф-ций; графики наиболее часто используемых ф-ций приведены на рис. 1.
≈ при ≈! < ≈ :
(V. L IT ^ ∙> '
Л I * f 1
О при I≈ > ≈;
1 ≈ щслеобразная а (х) ≈
2 ≈ дифракг^ионная а(х) = ≈ [sm (3TXSt1 JJT Q;≈о,Ьои*о
3~гауссоиа а (д;) ≈ ≈ 1/ -^≈ ехр { ≈ 4 In 2 ^- \ :
∙* \\ ' ct f n \\_ a2 (
4≈треугольная а (х} ≈
о
при
при
5 ≈ дисперсионная а (х) = -(> ≈ экспоненциальная а(х)
а/2л
а
х
а
ехр ' ≈ 2'-^-!-
Все графики приведены к одной и той же ширине а. Под шириной А, ф. понимают разность абсцисс, при к-рых значения ф-ции в 2 раза миньте е╦ макс, значения. Часто ширину А, ф. наз. «полушириной», иногда «спектральной шириной щели» или реже «спектральной шириной А. ф.». Ширина А. ф. характеризует разрешающую способность спектрометра. Действительно, если расположить на расстоянии ширины дзе крииые, напр. гауссовой формы (рис. 2), их суммарная огибающая обладает, минимумом н центре, составляющем 0,92 от ее максимума. При этом можно считать, что две регистрируемых полосы излучения или поглощения разрешены. Т. о.т приближ╦нно предельное разрешение прибора равно предельно малой ширине его А. ф. При увеличении ширины А. ф. соответственно ухудшается разро-шсшю.
А, ф. оптич. прибора, создающего изображение (телескоп, микроскоп и др.)» описывает распределение освещ╦нности в создаваемом прибором изображении бесконечно малого (точечного) источника излучения. Идеальный оптич. прибор изображает точечный источник излучения в виде точки ф(.г, у), его А. ф. везде, кроме этой точки, равна нулю. Реальные онтич. приборы изображают точку в виде пятна рассеянной энергии; А. ф. таких приборов не равна нулю в области конечных размеров /(.с, у]. Величина этой области и вид А. ф, длн разных приборов различны. В безаберрац. приборах величина А. ф. определяется дифракцией света и может быть рассчитана для разных форм апор-турной диафрагмы. Углоные размеры области, в к-рий А. ф. отлична от нуля, по порядку величины равны KID, где \ ≈ длина полны, D ≈ размер входного зрачка (см. такжо Дифракционная расходимость). Аберрации и дефекты изготовления оптич. деталей приводят к дополнит. расширению области, в к-рой А. ф. отлична от нуля. Площадь конечных размеров f(x, у), к-рую занимает изображение точечного источника реальным прибором, является в этом случае А. ф. этого оптич. прибора а(х, у]. Расч╦т А, ф. при наличии аберрации очень сложен и практически нв всегда возможен, поэтому часто с╦ определяют окспсрнм. пут╦м. А. ф. позволяет оценить разрешающую способность оптич. приборов: чем широ А. ф.т тем хуже разрешение, так жо как и для спектрометров. В табл. приводятся разрешающая способность и А. ф, нек-рых оптич. приборок.
")
}




